Matrix Factorization의 개념
-
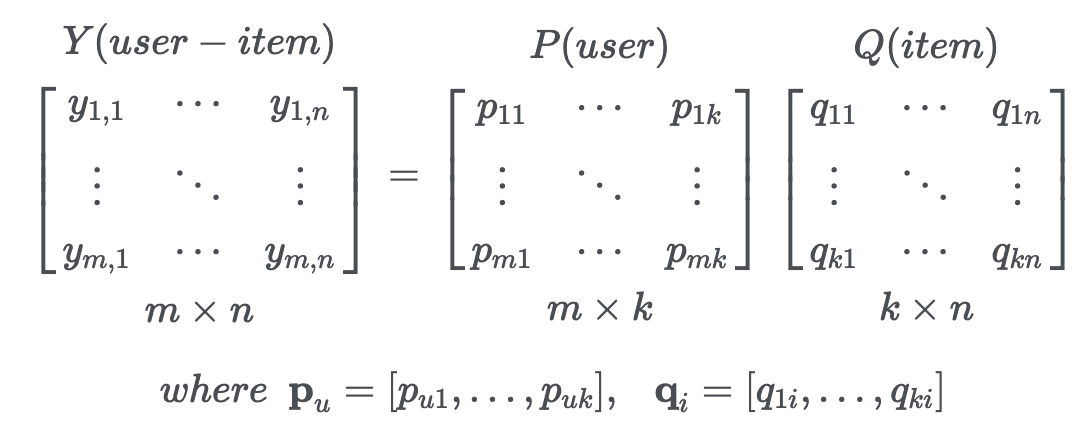
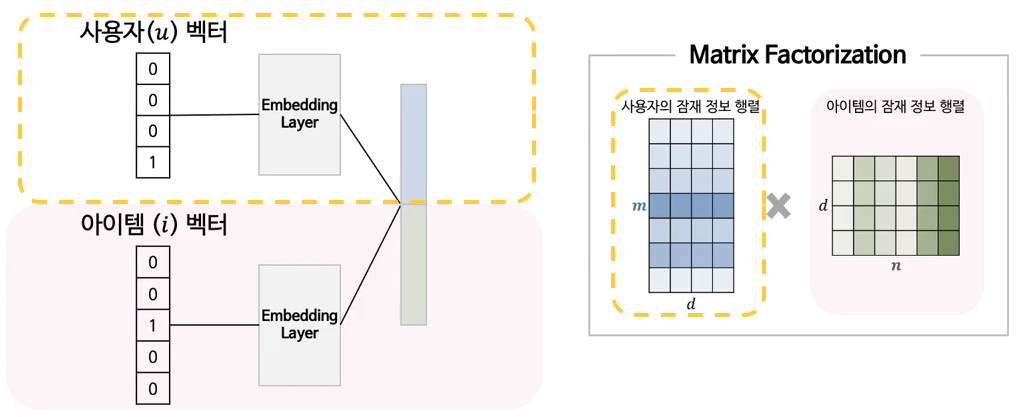
Collaborative Filtering 방식 중 한 종류로써 User-Item Matrix를 N차원의 User와 Item의 latent factor 행렬곱으로 분해하여 표현하는 방법
-
이때 y값의 예측은 latent feature들의 inner product를 통해 구함
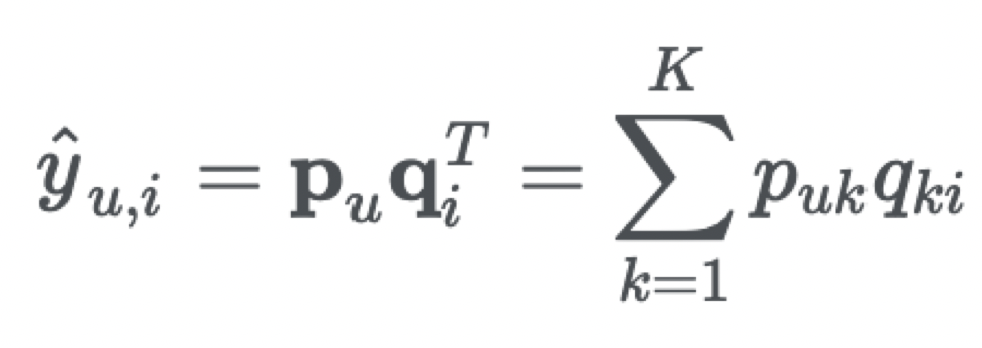
Matrix Factorization의 문제점
- Matrix Factorization에서 inner product는 단순한 방법으로 매우 효율적이지만 linear한 방식이므로 user와 item간의 복잡한 관계를 표현하는데 한계가 있음
 식으로 볼 수 있드시 결합할 시 linear하게 연산한다
식으로 볼 수 있드시 결합할 시 linear하게 연산한다- 더 높은 차원의 latent space를 도입한다면 더 복잡한 대소관계 표현이 가능해 질 것이다. 하지만 latent space의 차원을 증가시키는 것은 모델의 일반화 성능(generalization)을 저해할 수 있는 방법이다.
- 하지만 Deep Neural Network(DNN)의 multi-layer구조는 non-linear하기 때문에 보다 복잡한 구조를 표현하는데 용이함
Neural Collaborative Filtering (NCF)
- 본 논문에서는 Implicit feedback을 활용하여 신경망을 학습합니다.
- Implicit feedback은 관계 파악이 어렵지만, 많은 양의 데이터를 구할 수 있기 때문에 신경망 구조의 유효성을 검증하기에 알맞다고 할 수 있습니다.
NCF의 구조
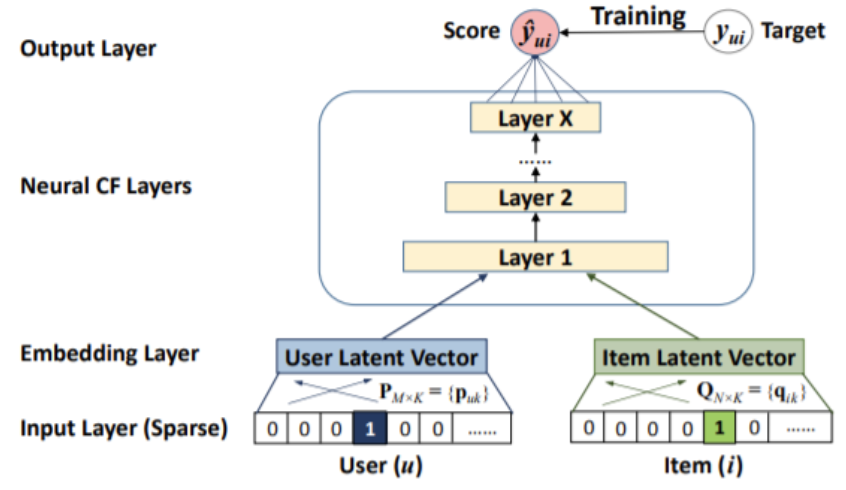
Input Layer
-
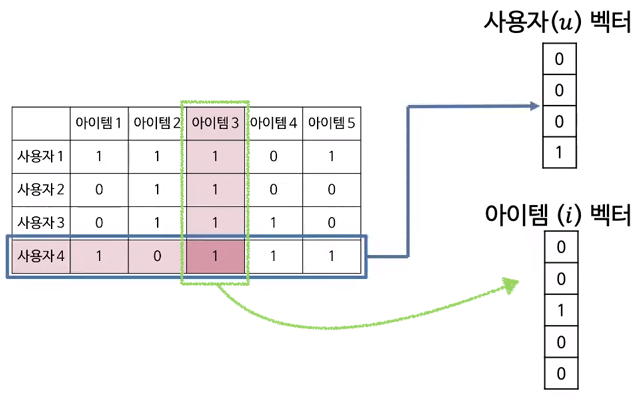
user와 item이 one-hot encoding으로 표현되어 매우 sparse한 상태의 vector임
Embedding Layer
-
Embedding : 범주형(Categorical) 자료를 연속형(Continuous) 벡터로 치환하는 것
- 범주형 자료 : 관측 결과가 몇개의 범주 또는 항목의 형태로 나타내는 자료 (ex. Boolean)
- 연속형 자료 : 연속된 구간의 값을 가지는 자료 (ex. 키, 몸무게)
-
Embedding layer에서는 Fully-connected layer를 통해 Input Layer의 vector를 기반으로 dense vector를 얻을 수 있음
-
Embedding 과정이 Matrix Factorization에서의 latent factor vector와 같은 역할을 한다고 볼 수 있음
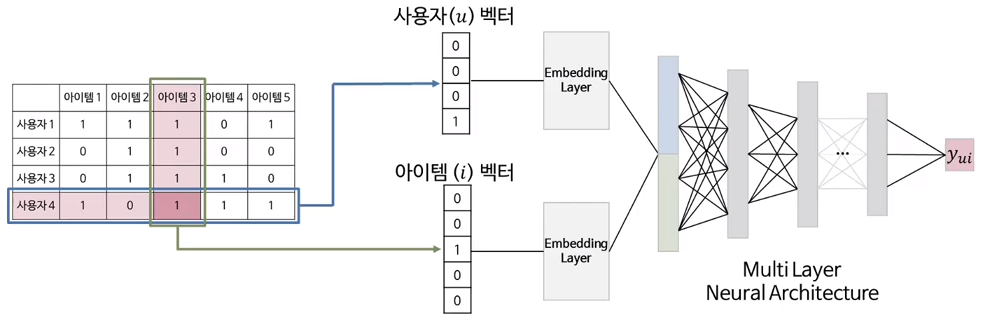
Neural CF Layers
- user embedding과 item embedding을 latent factor로 보고 그 두 개의 vector를 concatenate하여 Neural net에 넣게됨
- 각각의 층을 거치며 인공신경망을 통해 복잡한 비선형의 데이터 관계를 학습할 수 있게 됨
Output Layer
-
y_ui에 대해 예측을 하게 되는데. 예측값은 0과 1 사이의 값으로 user u와 item i가 얼마나 관련 있는지를 나타냄
NCF 훈련
-
Optimizer로는 SGD
-
Loss function으로는 binary cross entropy loss
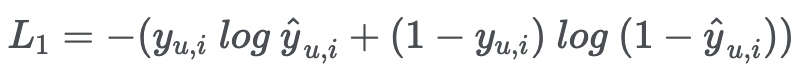
- 실제값이 y_ui = 1인데 예측값이 ^y_ui = 0이라면, L1 = ∞
- 실제값이 y_ui = 1인데 예측값이 ^y_ui = 1이라면, L1 = 0
Neural Matrix Factorization (NeuMF)
- GMF와 MLP를 결합한 Model
Generalized Matrix Factorization (GMF)
-
제안한 NCF 구조에서 이뤄지는 Matrix Factorization
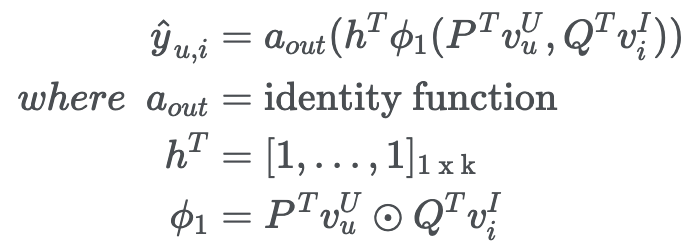
-
a_out을 identical function, h를 [1,1,1,….] 형태의 uniform vector로 가정한다면 NCF 구조는 Matrix Factorization과 동일함
-
즉, NCF 구조에서 Matrix Factorization는 쉽게 일반화와 확장이 가능
-
논문 저자가 설정한 확장 버전 :
Symbol a_out Activation Function - Sigmoid h^T 각 텀에 각기 다른 가중치를 줄 수 있도록 하였다, 이는 latent vector의 중요도를 조절하는 역할을 하게 됨 ϕ_1 Element-wise product function
-
Multi-Layer Perceptron (MLP)
-
GMF같은 경우 linear하고 fixed한 특징으로 인해 User과 Item 간의 복잡한 interaction 관계를 표현하지 못한다고 함
-
User과 Item 간의 복잡한 interaction 관계를 학습하기 위해서 hidden layer를 여러 개 추가함으로써 flexibility하고 non-linearity한 딥러닝의 장점을 모델에 적용할 수 있음
- 실험을 통해 layer가 깊어질수록 높은 성능을 보이고 있음을 알 수 있음
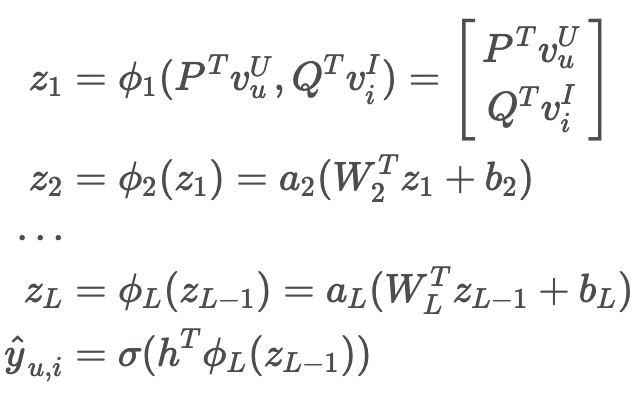
Symbol a_x Activation Function - 경험을 통해 ReLU가 가장 좋았음 W_x weight matrix b_x bias vector ϕ_1 concatenation function (결합시켜주는 함수) σ Sigmoid function
NeuMF 전체 구조
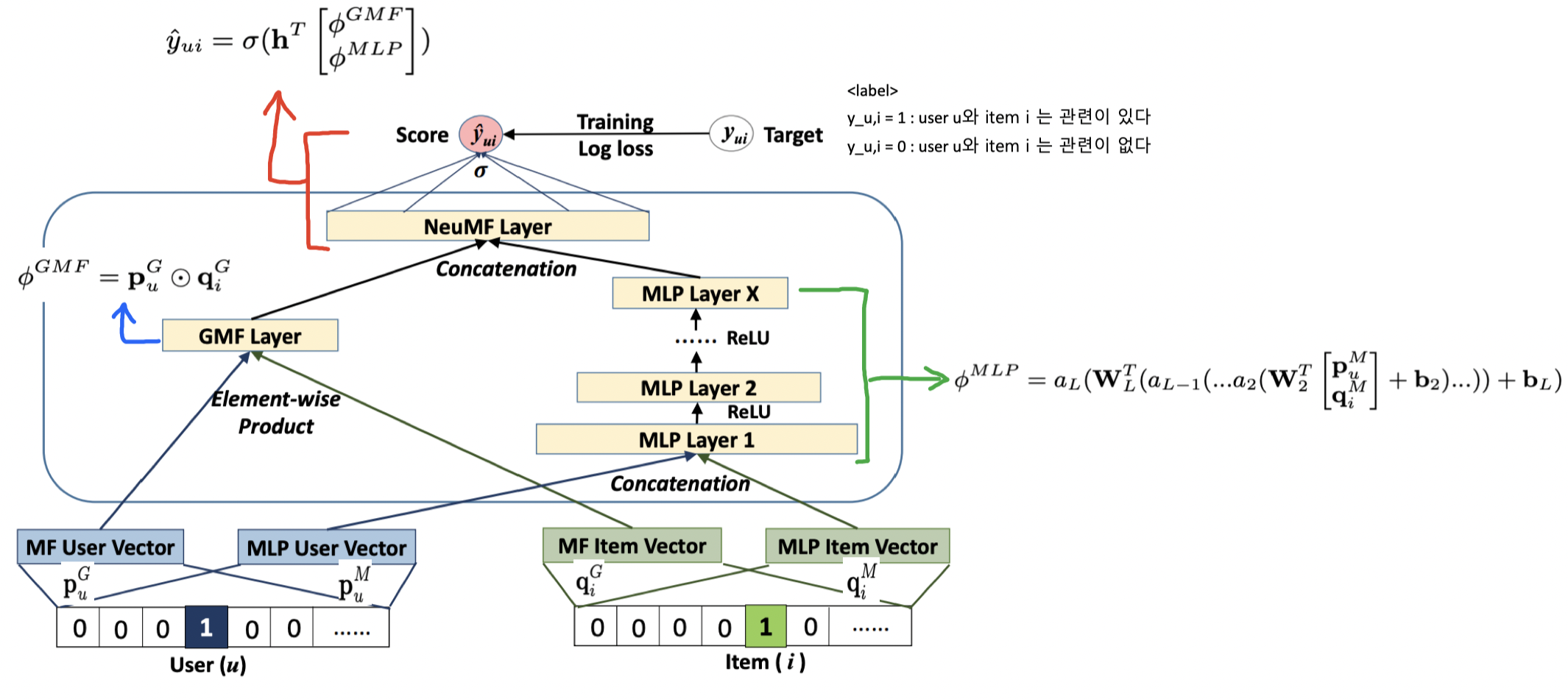
- 이 모델은 user-item간의 상호 관계를 표현하기 위해 Matrix Factorization의 linearity 와 Multi-Layer Perceptron의 non-linearity를 결합한 것이 특징
- linear space에 기반한 기존 모델들이 갖는 한계를 DNN을 도입해 해결하면서 NeuMF은 Collaborative Filtering의 핵심 가치를 놓치 않으면서 성능은 높인 방법
NeuMF 훈련
- GMF와 MLP를 Random initialization으로 parameter를 수렴할 때 까지 훈련시킴
- 훈련된 GMF와 MLP의 parameter를 NeuMF에서 활용