Vanila GAN의 개념
확률 분포
-
확률변수 : 무작위 실험을 했을 때, 특정 확률로 발생하는 각각의 결과를 수치적 값으로 표현하는 변수
- 주사위를 던졌을 때 나올 수 있는 확률변수 : 1, 2, 3, 4, 5, 6
-
확률분포 : 확률변수가 특정한 값을 가질 확률을 나타내는 함수
-
이산확률분포 : 대표적으로 주사위 눈금의 확률 분포
-
연속확률분포 : 대표적으로 정규 분포(Gaussian distribution)
-
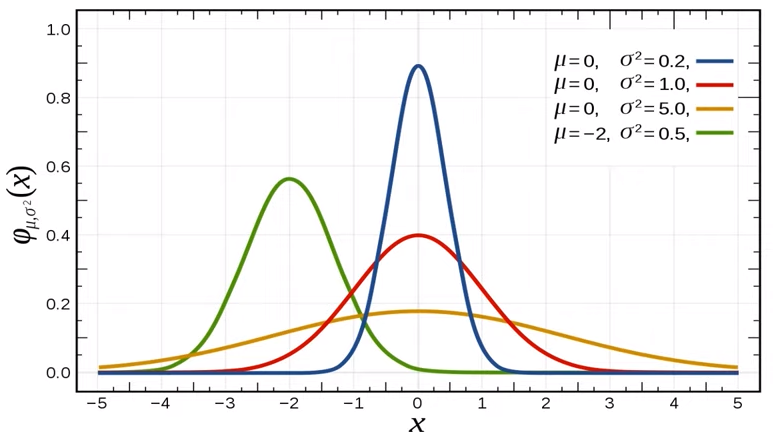
Image Data에 대한 확률분포
-
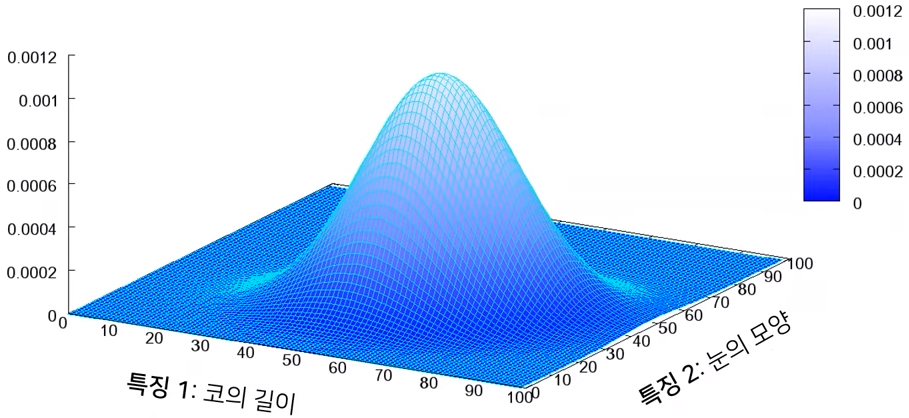
Image Data는 다차원의 feature space의 한 점으로 표헌됨
-
사람의 얼굴에는 통계적인 평균치가 존재할 수 있음
- ex. 눈의 길이, 코의 길이, 목의 두께, 눈썹의 길이 등등
-
Image Data에 대한 확률분포 : 이미지에서의 다양한 feature들이 각각의 확률변수가 되는 분포
Vanila GAN 구조
- 머신러닝은 크게 3가지 개념 지도학습/강화학습/비지도학습 으로 분류되는데, GAN은 ‘비지도 학습’에 해당됨
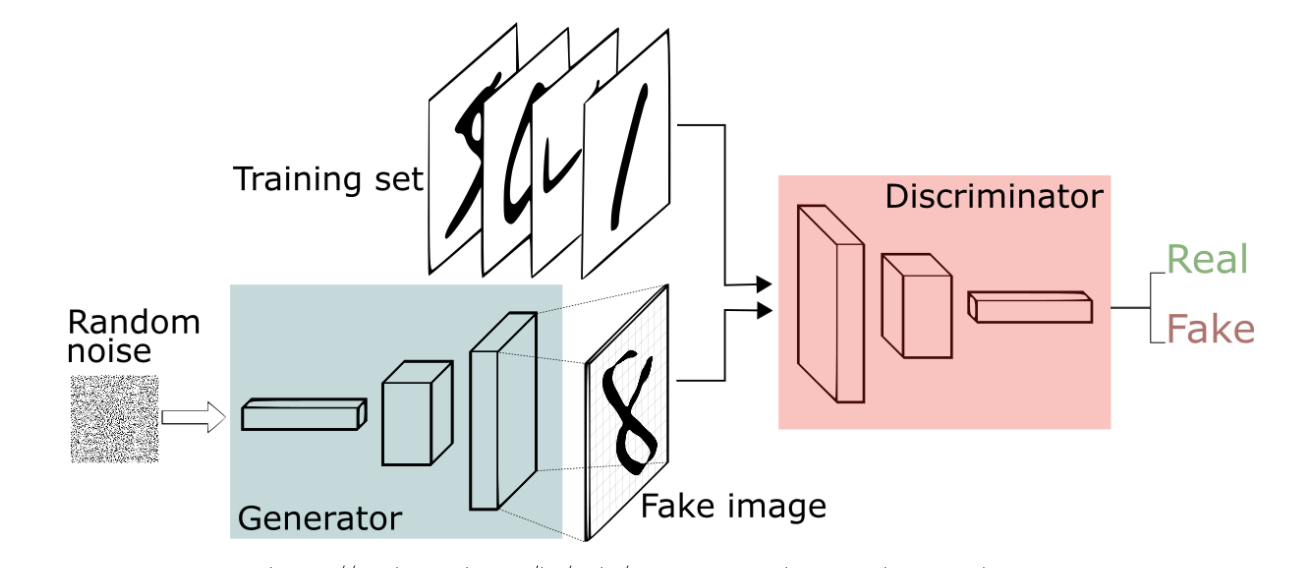
Generator
-
Generator는 학습 데이터의 분포(distribution)를 알아내도록 학습함.
-
Generator가 학습이 잘 됬을 경우, 확률값이 높은 부분의 변수(이미지)를 sampling할 때 있을 법한 이미지가 나오게됨
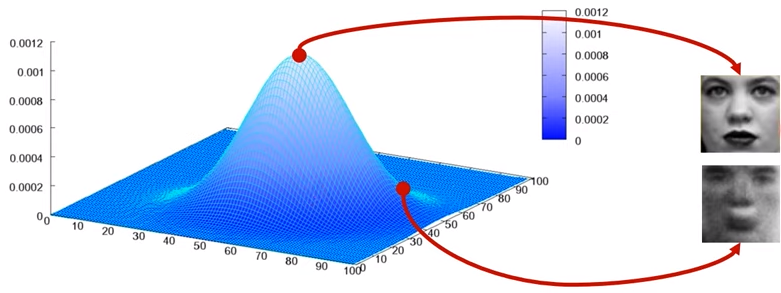
- Generator가 분포를 잘 학습한 다음에 확률이 높은 부분 부터 출발해서 약간의 noise를 섞어가면서 랜덤하게 sampling을 한다면 다양한 형태로 그럴싸한 image들을 생성할 수 있음
Discriminator
- Discriminator는 실제 데이터인지 가짜 데이터인지 구별해서 각각에 대한 확률을 추정함
GAN을 통해 이루고자 하는 목표 :
- Generator의 분포가 원본 학습데이터의 분포를 잘 따를 수 있도록 만드는 것
- Discriminator가 학습이 다 된 경우 가짜 이미지와 진짜 이미지를 더 이상 구분할 수 없어서 항상 1/2 (50%) 이라는 값을 output하도록 하는 것
Vanila GAN의 문제점
- Vanila GAN은 단순한 image (MNIST, CIFAR-10)는 괜찮은 image를 생성하였지만 복잡한 영상에 대해서는 좋은 image를 생성하지 못함
- Training시 안정성이 떨어지는 문제가 존재함
DCGAN 구조
DCGAN의 Guidelines
-
Generator
- Pooling Layer 대신 Fractional-Strided Convolution을 사용
- Batch Normalization을 적용
- Fully Connected Hidden layer를 제거
- Activation Funciton을 Output Layer에선 Tanh를 사용하고 나머지 Layer는 ReLU를 사용
-
Discriminator
- Pooling Layer 대신 Strided Convolution을 사용
- Batch Normalization을 적용
- Fully Connected Hidden layer를 제거
- Activation Function을 Leaky ReLU 사용
Generator의 output layer와 Discriminator의 input layer에는 Batch Normalization을 넣지 않았다
DCGAN 모델 구조
-
Generator
-
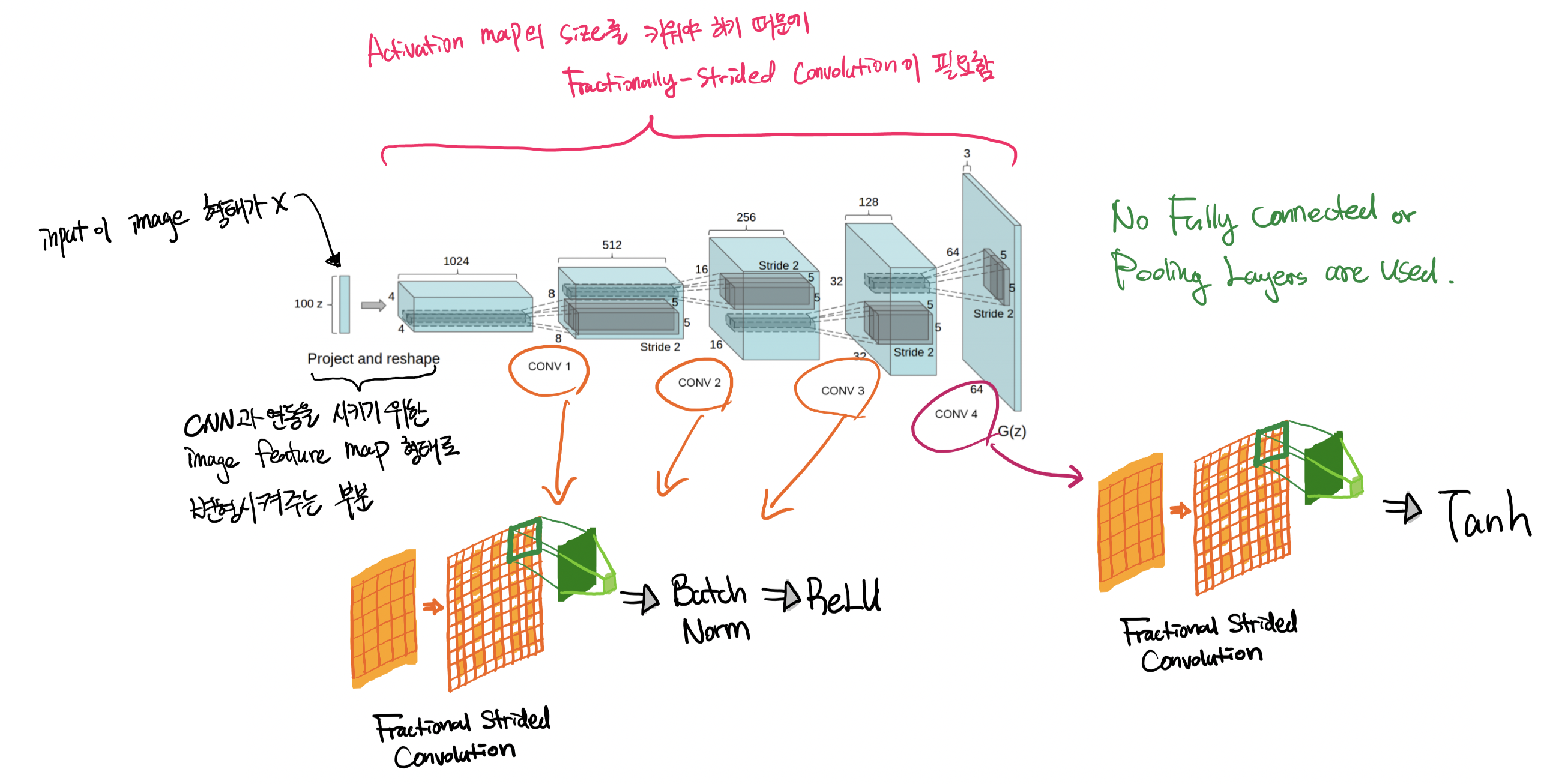
Input size : (100, 1, 1) ➡️ Output size : (3, 64, 64)
-
Fractional-Strided Convolution (Transposed Convolution) :
-
Strided Convolution : Stride값을 1이상의 정수값을 사용하면 Pooling 처럼 출력되는 Activation map의 size를 줄이는 효과를 얻을 수 있음
-
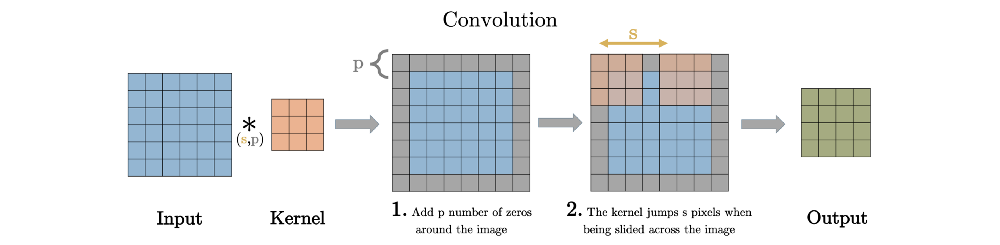
Fractional-Strided(즉 Stride 값을 1보다 작은 분수)를 사용하는 경우 Activation map의 size를 키울수 있는 효과를 얻을 수 있음
-
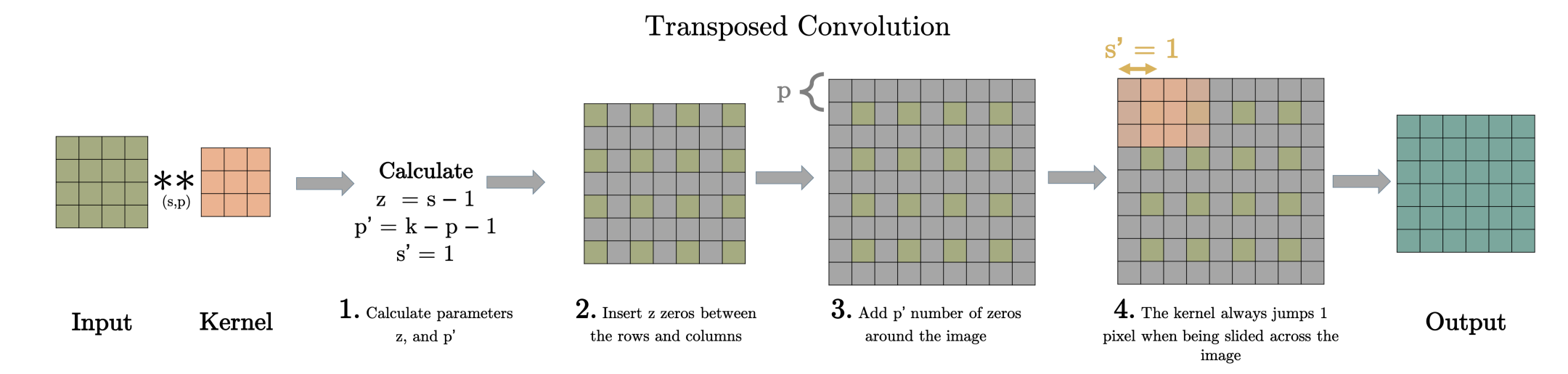
새로운 parameter z, 와 p′을 계산
-
input의 각 행과 열 사이에 z 만큼의 0을 삽입
- 이 단계에서 input의 사이즈를 (2∗input−1) x (2∗input−1)만큼 증가시킴
-
전 단계에서 변형된 input에다 p′ 만큼의 0을 padding 해줌
-
전 단계에서 변형된 input에다 stride 1인 일반적인 convolution을 진행
-
-
Pooling 등을 통해 이미지를 축소시키면서 데이터를 압축했다면, 그 데이터를 다시 원래의 이미지로 복원하기 위해 이미지를 크게 만들어야(Up-sampling)하는데, 이럴 때 사용되는 방법
-
단순히 이미지의 해상도를 높이는 Super resolution 에서도 많이 쓰인다
-
-
Code (Pytorch) :
import torch import torch.nn as nn class Generator(nn.Module): def __init__(self, z_dim, channels_img, features_g): super(Generator, self).__init__() self.gen = nn.Sequential( # input shape : z_dim * 1 * 1 self._block(z_dim, features_g*16, 4, 1, 0), # become 4 * 4 self._block(features_g * 16, features_g * 8, 4, 2, 1), # become 8 * 8 self._block(features_g * 8, features_g * 4, 4, 2, 1), # become 16 * 16 self._block(features_g * 4, features_g * 2, 4, 2, 1), # become 32 * 32 nn.ConvTranspose2d( features_g * 2, channels_img, kernel_size=4, stride=2, padding=1 ), nn.Tanh(), ) def _block(self, in_channels, out_channels, kernel_size, stride, padding): return nn.Sequential( nn.ConvTranspose2d( in_channels, out_channels, kernel_size, stride, padding, bias=False, ), nn.BatchNorm2d(out_channels), nn.ReLU(), ) def forward(self, x): return self.gen(x)
-
-
Discriminator
-
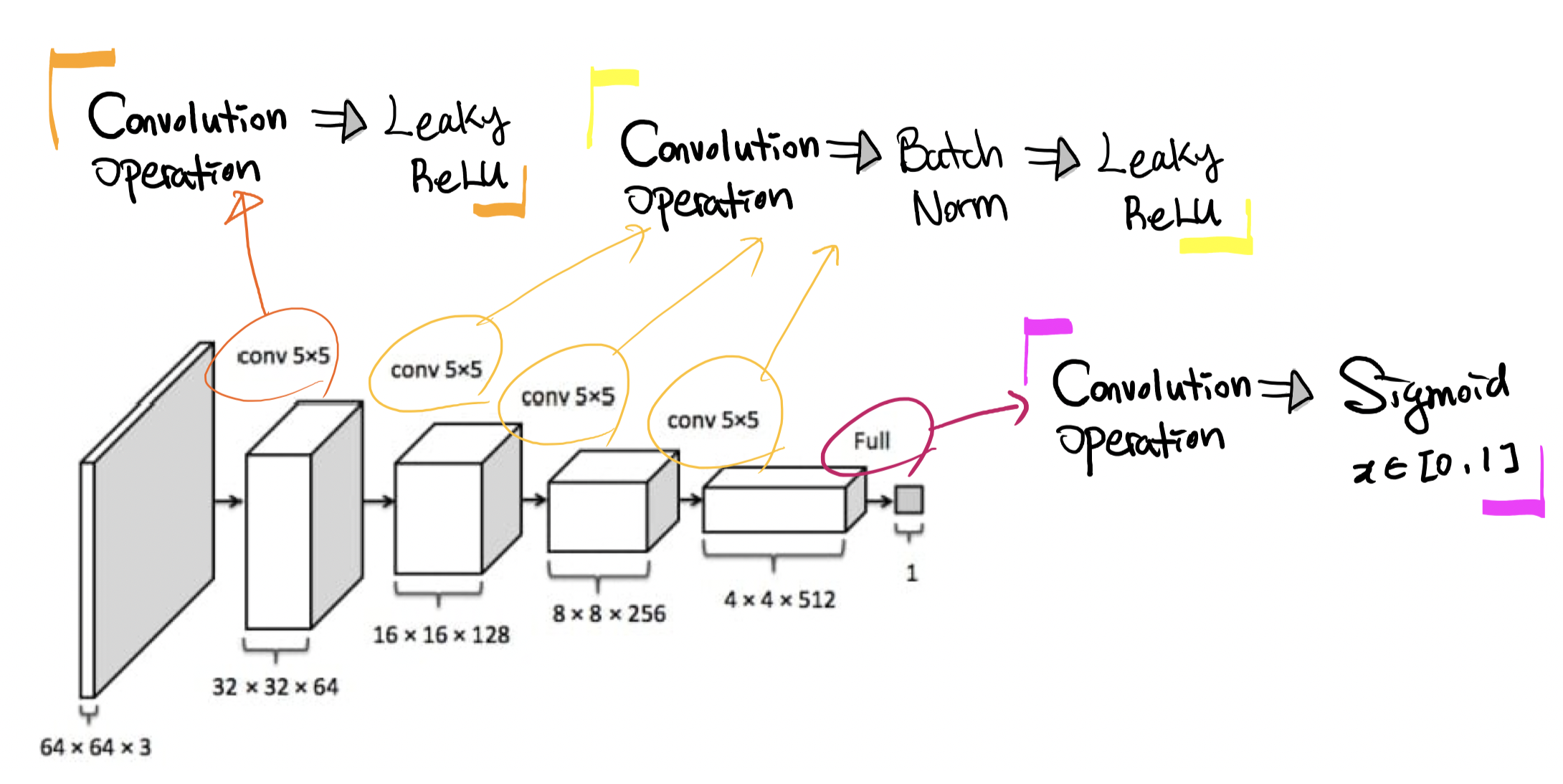
Input : (3, 64, 64) ➡️ Output : (1, 1, 1)
-
Code (Pytorch) :
import torch import torch.nn as nn class Discriminator(nn.Module): def __init__(self, channels_img, features_d): super(Discriminator, self).__init__() self.disc = nn.Sequential( # input shape : channels_img * 64 * 64 nn.Conv2d( channels_img, features_d, kernel_size=4, stride=2, padding=1 ), # become 32 * 32 nn.LeakyReLU(0.2), self._block(features_d, features_d*2, 4, 2, 1), # become 16 * 16 self._block(features_d*2, features_d*4, 4, 2, 1), # become 8 * 8 self._block(features_d*4, features_d*8, 4, 2, 1), # become 4 * 4 nn.Conv2d(features_d*8, 1, kernel_size=4, stride=2, padding=0), # become 1 * 1 nn.Sigmoid(), ) def _block(self, in_channels, out_channels, kernel_size, stride, padding): return nn.Sequential( nn.Conv2d( in_channels, out_channels, kernel_size, stride, padding, bias=False, ), nn.BatchNorm2d(out_channels), nn.LeakyReLU(0.2), ) def forward(self, x): return self.disc(x)
-
DCGAN 훈련
Weight Initialization
-
All weights were initialized from a zero-centered Normal distribution with standard deviation 0.02
-
Code (Pytorch) :
def initialize_weights(model): for m in model.modules(): if isinstance(m, (nn.Conv2d, nn.ConvTranspose2d, nn.BatchNorm2d)): nn.init.normal_(m.weight.data, 0.0, 0.02)
Hyperparameters
-
LEARNING_RATE = 2e-4: We found the suggested learning rate of 0.001, to be too high, using 0.0002 instead. -
BATCH_SIZE = 128: 모든 모델은 mini-batch stochastic gradient descent(SGD)에서 batch size 128로 훈련됨 -
nn.LeakyReLU(0.2): Leaky ReLU의 기울기는 0.2 -
hyperpameter를 변경한 Adam optimizer를 사용함.
optimizer_gen = optim.Adam(gen.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999)) optimizer_disc = optim.Adam(disc.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999))- learning rate 0.001은 너무 높고 0.0002가 적당하다는 점을 찾았고,
- momentum B1은 0.9에서 트레이닝이 변동성이 크고 불안정한 반면 0.5에서 트레이닝이 안정적이었다.
Training Algorithm
-
Batch와 Mini-batch gradient descent에 대한 개념 정리 : Blog
-
MinMax Loss :
- Ex~pdata(x)[logD(x)] 는 training data(real data) x를 Discriminator에 넣었을 때 나오는 결과를 log를 취했을 때 얻는 기댓(평균)값을 의미한다.
- Ez~px(z)[log(1-D(G(z)))] 는 noise distribution z를 Generator에 넣었을 때 나오는 결과(fake image)를 Discriminator에 넣는다. 그 결과를 log (1 - Discriminator 결과값)를 했을 때 얻는 기댓(평균)값을 의미한다.
- 만약에 D가 매우 뛰어난 성능을 보이고 있다고 가정한다. D에 들어온 sample x가 실제로 real_data에서 온 sample일 경우 D(x) = 1이 되므로 첫 번째 항에서 ‘log 1 = 0’ 이 되어 사라진다. 그리고 G(z)가 생성한 fake_image를 잘 판별할 수 있어서 D(G(z)) = 0이라는 결과를 나타내어 두 번째 항에서 ‘log (1 - 0) = log 1 = 0’이 되어 식 전체 값은 0이 된다. 따라서 L(D,G) = 0이 D의 입장에서 얻을 수 있는 ‘최댓값’이라는 것을 알 수 있다.
- 반대로 이번에는 G가 아무도 못알아보게끔 image를 잘 생성한다고 가정한다. 일단 G는 첫 번째 항에는 관여할 수 없다. 오로지 D가 real_data로 부터 나온 sample x를 얼마나 잘 판별하는지에 대한 항이기 때문이다. G의 입장에서 확인해야할 항은 두 번째 항이다. G가 매우 뛰어난 성능을 보여 D를 무조건 속인다고 가정했기 때문에 D(G(z))에서 D는 real이라고 판단해서 1의 결론을 내놓습니다. 따라서 ‘log (1 - 1) = -∞’ 라는 결과가 나오게 된다. 즉 L(D,G)=-∞ 는 G의 입장에서 얻을 수 있는 ‘최솟값’이라는 것을 알 수 있다.
-
Vanila GAN Training Algorithm :
-
Outer Loop 1번 진행 : 1 iteration(특정 batch size의 mini_batch를 가지고 front&back prop.를 1회 진행)에 Discriminator와 Generator의 parameter를 update한다
- Inner Loop : Discriminator update k번 (k는 Hyperparameter)
- Generator update 1번
Discriminator와 Generator의 parameter가 수렴하기 위해서 iteration을(or Outer Loop) 얼마나 설정해야될까?- Training for longer will probably lead to better results but will also take much longer (Pytorch Tutorial)
# Number of training epochs EPOCHS = 5 Algorithm에서 왜 Discriminator를 Generator보다 더 많이 훈련시키는거지?- if the discriminator is already calling generator’s images as real, generator does not have any incentive to do any better (Quora.com)
위에 Algorithm에서 Discriminator를 1 iteration마다 한번만(k=1) 훈련시킨 이유 :- In most experiments, we don’t find much benefit (or harm) from running the discriminator for multiple steps. Running discriminator truly to convergence would be extremely expensive. (Quora.com)
-
Outer Loop 1번 진행 : 1 iteration(특정 batch size의 mini_batch를 가지고 front&back prop.를 1회 진행)에 Discriminator와 Generator의 parameter를 update한다
-
Code(Pytorch) :
import torch import torch.nn as nn import torch.optim as optim import torchvision import torchvision.datasets as datasets import torchvision.transforms as transforms from torch.utils.data import DataLoader from model import Discriminator, Generator, initialize_weights # Hyperparameters etc. device = torch.device("cuda" if torch.cuda.is_available() else "cpu") LEARNING_RATE = 2e-4 BATCH_SIZE = 128 IMAGE_SIZE = 64 CHANNEL_IMG = 1 Z_DIM = 100 EPOCHS = 5 FEATURES_disc = 64 FEATURES_gen = 64 transforms = transforms.Compose( [ transforms.Resize(IMAGE_SIZE), transforms.ToTensor(), transforms.Normalize( [0.5 for _ in range(CHANNEL_IMG)], [0.5 for _ in range(CHANNEL_IMG)] ) ] ) print("===================== [STARTING] LOADING DATA =====================") dataset = datasets.MNIST(root="dataset/", train=True, transform=transforms, download=True) loader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True) print("===================== [FINISHED] LOADING DATA =====================") gen = Generator(Z_DIM, CHANNEL_IMG, FEATURES_gen).to(device) disc = Discriminator(CHANNEL_IMG, FEATURES_disc).to(device) print("===================== [STARTING] WEIGHT INIT =====================") initialize_weights(gen) initialize_weights(disc) print("===================== [FINISHED] WEIGHT INIT =====================") optimizer_gen = optim.Adam(gen.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999)) optimizer_disc = optim.Adam(disc.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999)) criterion = nn.BCELoss() fixed_noise = torch.randn(32, Z_DIM, 1, 1).to(device) gen.train() disc.train() print("===================== [STARTING] MODEL TRAINING =====================") for epoch in range(EPOCHS): for batch_index, (real, _) in enumerate(loader): # _ : we don't need label real = real.to(device) noise = torch.randn((BATCH_SIZE, Z_DIM, 1, 1)).to(device) fake = gen(noise) # Train Discriminator max log(D(x)) + log(1 - D(G(z))) disc_real = disc(real).reshape(-1) # N * 1 * 1 * 1 ==> N loss_disc_real = criterion(disc_real, torch.ones_like(disc_real)) disc_fake = disc(fake).reshape(-1) loss_disc_fake = criterion(disc_fake, torch.zeros_like(disc_fake)) loss_disc = (loss_disc_real + loss_disc_fake) / 2 disc.zero_grad() loss_disc.backward(retain_graph=True) optimizer_disc.step() # Train Generator min log(1 - D(G(z))) ⟷ max log(D(x)) output = disc(fake).reshape(-1) loss_gen = criterion(output, torch.ones_like(output)) gen.zero_grad() loss_gen.backward() optimizer_gen.step() print("===================== [FINISHED] MODEL TRAINING =====================")
추가적인 내용
- input인 noise(z)는 별 의미 없는 값이 아니라, 이것이 생성될 이미지의 특징을 결정하는 벡터이다. 논문에서는
- 웃는 여자를 생성한 noise z1
- 무표정 여자를 생성한 noise z2
- 무표정 남자를 생성한 noise z3
- z4 := z1 - z2 + z3이라 할 때, z4를 noise로 쓰면 웃는 남자를 생성해낸다.