Recursions, Dynamic programming, Sorting, Graph

Recursions

재귀 호출
Examples
- GCD
  - Euclid’s Algorithm
    
    GCD(A, B) = GCD(B, A mod B) GCD(A, 0) = A
Stack Frame : Function call의 진행된 역사를 기록하고 stack
- 함수가 호출되면 Push
- 함수가 return하면 Pop
- 지역 변수와 함수 parameter가 저장됨
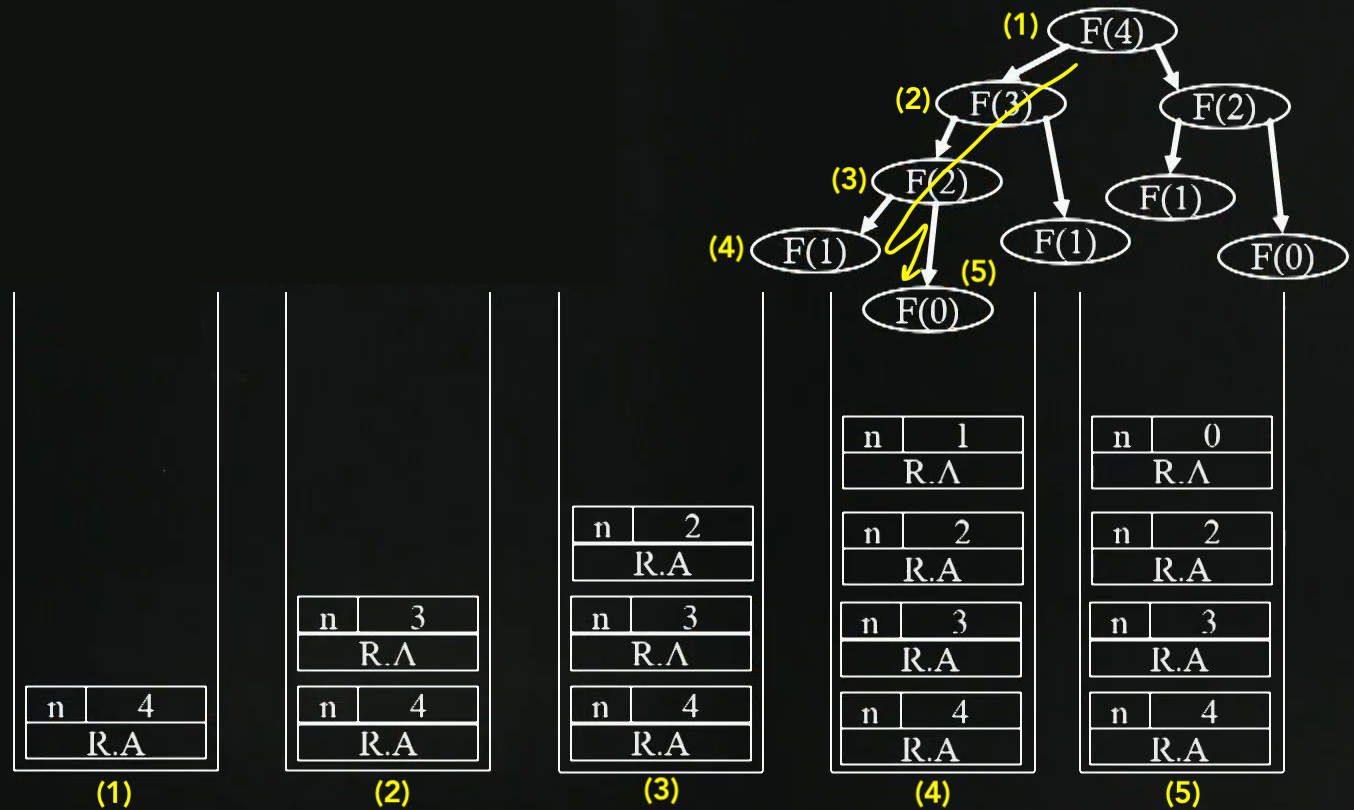
  - Return Address(R.A) : 이 Address속에 어떤 함수가 call되었는가가 저장되어있음
Recursion의 문제점 :
- 같은 parameter로 같은 함수를 call하게되면 불필요하게 시간과 공간만 더 쓰게 됨
  - Fibonacci(4) 의 경우 Fibonacci(1)만 3번을 호출함.
  - 즉, 동일한 값을 갇기위해서 왜 여러번 함수 call을 해야되나
- 해결방법 : Dynamic programming
  - 많은 함수 call을 제거하기 위해, 1번 call하고 call된 결과를 기록함

Iteration Recursion

Recursion는 stack이라는 메모리 공간을 사용하는데, 반복적으로 자기 자신을 부르면서 stack에 계속해서 자기 자신이 쌓여가기 때문에 성능이 좋지 않다.
- 무한 Recursion이 발생할 경우 메모리의 제한이 있는 한 stack overflow가 뜨면서 프로그램이 비정상 종료된다.
Iteration의 경우엔 stack 메모리를 이런식으로 사용하지 않아 프로그램이 종료되지 않고 무한 실행된다

⁉️ Recursion를 따지고 보면 반복문보다 좋은 점이 없어 보인다.. 그럼에도 불구하고 Recursion를 사용하는 이유는?

알고리즘 자체가 재귀적인 표현이 자연스러운 경우 (ex. 피보나치 수열 점화식) 에 재귀함수를 쓰는 것이 유용
변수 사용을 줄여줄 수 있고 가독성이 향상
성능만 본다면 Iteration에 비해 메모리나 속도 등 성능적 측면에서 많이 뒤쳐져 Recursion는 사용하지 않는게 맞다.
H/W가 좋지 못해 S/W 속도를 극한까지 끌어올려야 하는 시대가 아니기에 협업하는 상황을 생각하면 가독성도 고려해 프로그래밍을 해야하기 때문에 프로그램의 목적을 고려하여 Recursion를 사용하는 것이 올바르다

Dynamic programming

Recursions에 의해서 나오는 다양한 함수 호출 결과를 다시 재활용하는 컨셉
- 이렇게 해서 실행 시간을 빠르게 만들어 줌
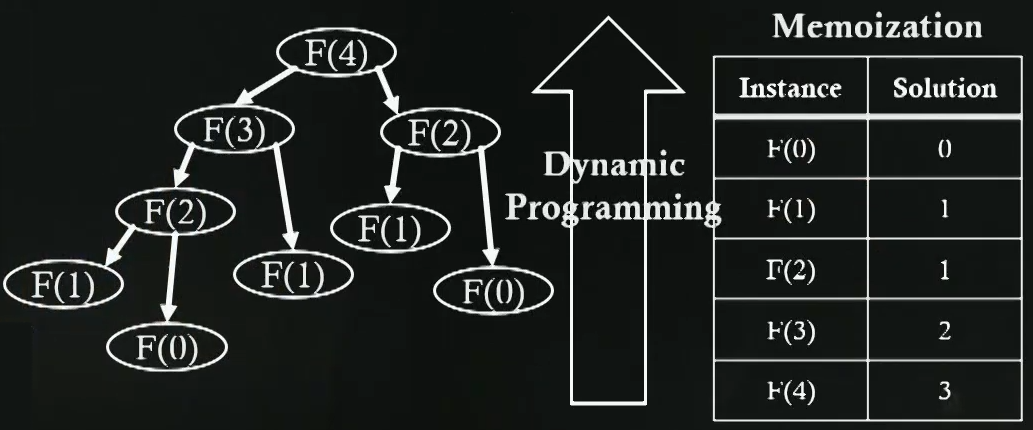
Memoization : Key technique of dynamic programming
- 기존의 function call과 그 것의 result를 재활용하기 위해서 result를 저장
- dynamic programming으로 Fibonacci 구현

Sorting Methods

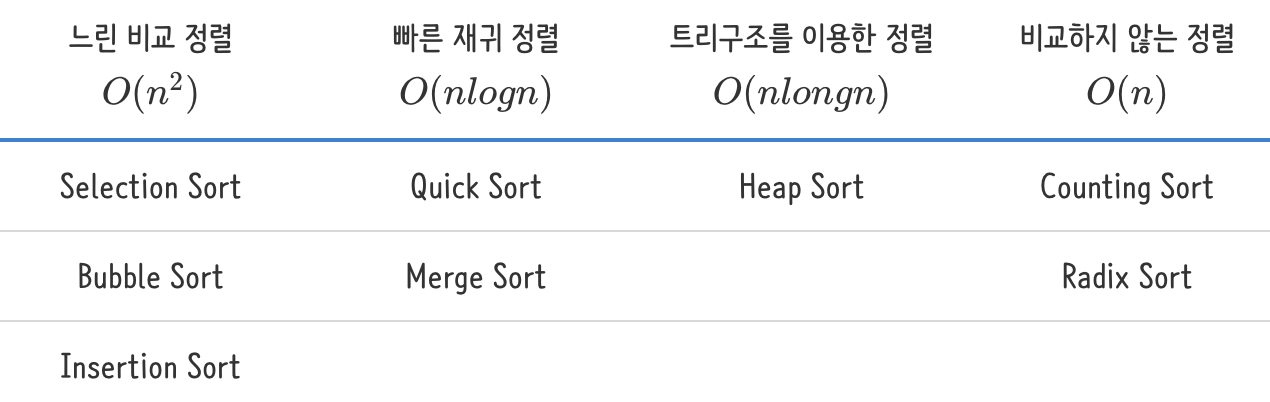
Screen Shot 2021-08-16 at 9.04.08 PM

O(n^2) Sorting

가장 효율적이지 못함, 하지만 구현하기 쉬움
Divide and conquer접근법이 적용되지 않음
- Divide and conquer :문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다. 분할 정복 방법은 대개 재귀를 이용하여 구현한다
두개의 Index를 활용한 comparison 접근법이 적용됨

Selection sort

주어진 리스트 중에 최소값을 찾는다.
그 값을 맨 앞에 위치한 값과 교체한다(pass)
맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다

Ex) list = { 21, 25, 49, 25*, 16, 08 }

public static void SelectionSort(int[] a, int n){
  for(int size=n; size>1; size--){
    int j = findMax(a,size);
    swap(a[j],a[size-1]);
  }
}

Bubble sort

인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환

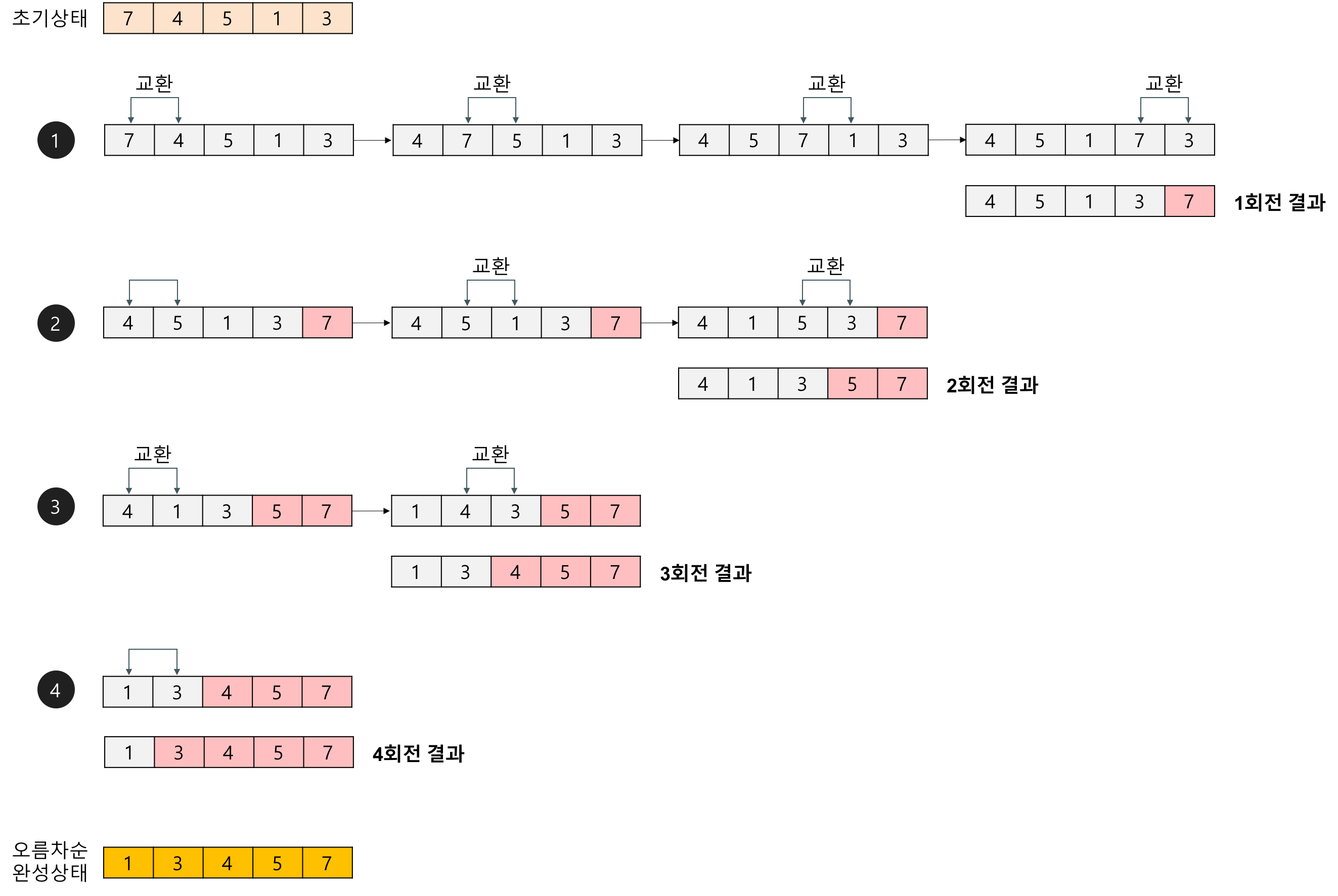
bubble-sort

# 오름차순
def bubbleSort(x):
	length = len(x)-1
	for i in range(length):
		for j in range(length-i):
			if x[j] > x[j+1]:
				x[j], x[j+1] = x[j+1], x[j]
	return x

Insertion Sort

현재 위치의 원소를 이미 정렬이 된 배열의 알맞은 위치에 삽입한다
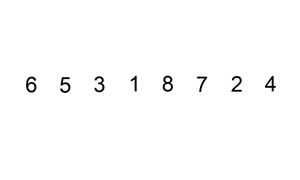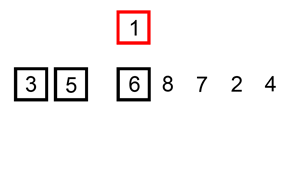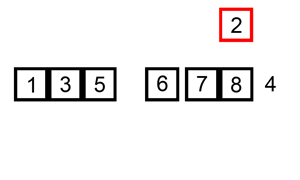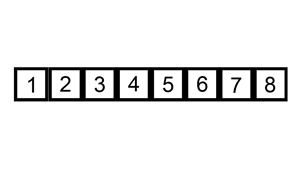
현재 List의 데이터가 거의 정렬 되어있는 상태라면 매우 빠르게 동작
Binary Search : Binary Search는 반드시 정렬이 된 상태의 Array에서 사용이 가능하다
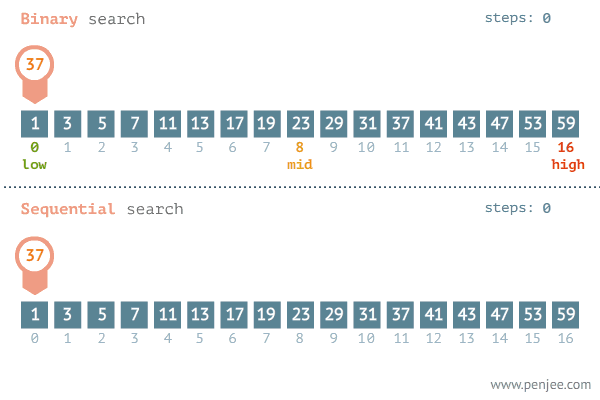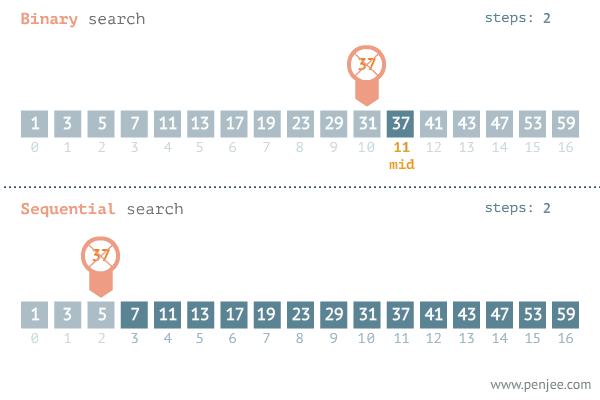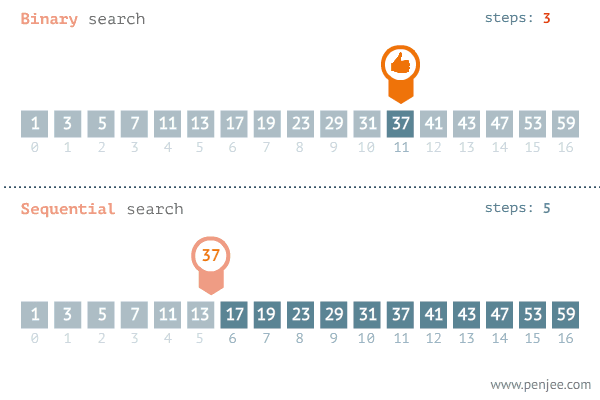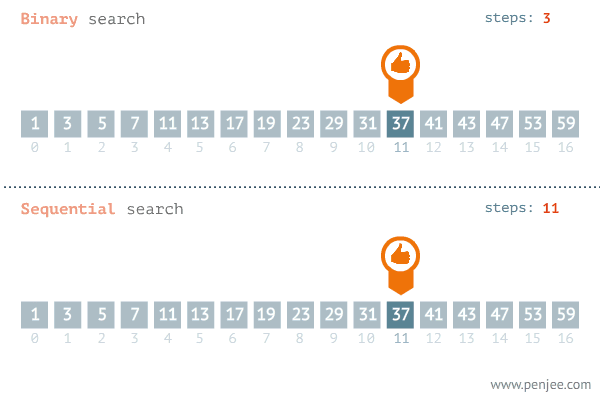
Insertion Sort에서 현재 위치의 원소를 이미 정렬이 된 배열의 알맞은 위치에 삽입을 할 때, 알맞은 위치를 찾는 방법으로 Binary Search를 사용하면 된다

예제 Video

O(n log n) Sorting

target sequence를 여러 개의 sequence로 나눠서 비교 하는 방법

Heap Sort

우선 Binary heap 의 Insert 를 통해 Binary heap을 형성
- worst case : O(log n)
  - 하나씩 Insert 할 때 마다 heap order update가 필요함
  - 가장 안좋은 경우는 새롭게 leaf node로 추가된 것이 업데이트를 하여 root node까지 가야되는 경우
  - log n == tree height
Heap Sort를 만들기 위해서 형성된 Binary heap에서 하나씩 꺼내면 됨
- Binary heap에서 하나씩 꺼낼때 마다 heap order update가 필요함

Quick Sort

리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라함

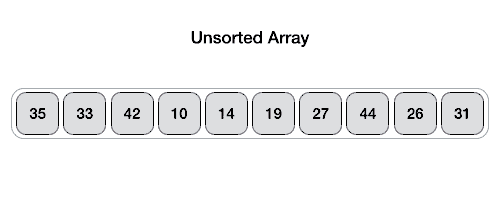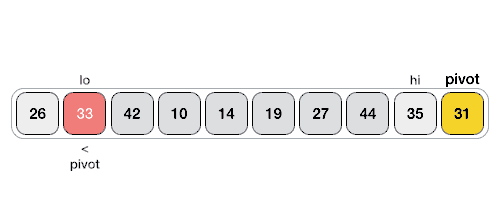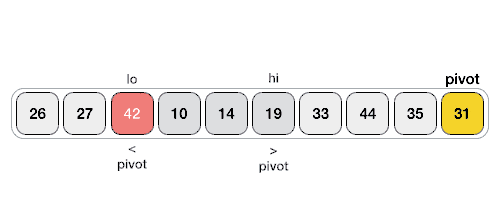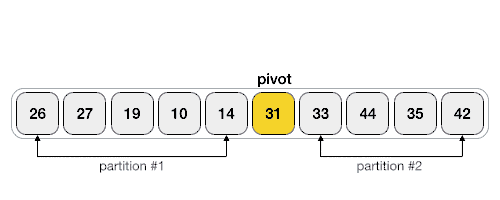
피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다

코드 예시에서는 위에 gif와는 다르게 Pivot을 첫번째 인덱스서 부터 시작함

 array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
   
 def quick_sort(array):
     # 리스트가 하나 이하의 원소만을 담고 있다면 종료
     if len(array) <= 1:
         return array
   
     pivot = array[0] # 피벗은 첫 번째 원소
     tail = array[1:] # 피벗을 제외한 리스트
   
     left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
     right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
   
     # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
     return quick_sort(left_side) + [pivot] + quick_sort(right_side)
   
 print(quick_sort(array))

최악의 시나리오 : Pivot의 분할이 절반에 가깝게 이루어지지 않고 한쪽 방향으로 편향된 분할이 될 경우

Merge Sort

더 작은 사이즈의 list로 줄이고 줄여서 한 숫자가 됬을 때 부터 비교해가면서 list를 합쳐나가는 과정

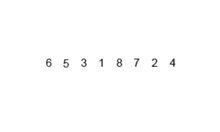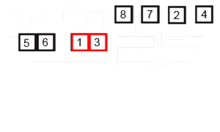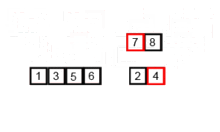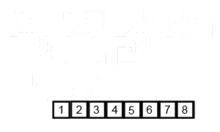
Merge-sort-example

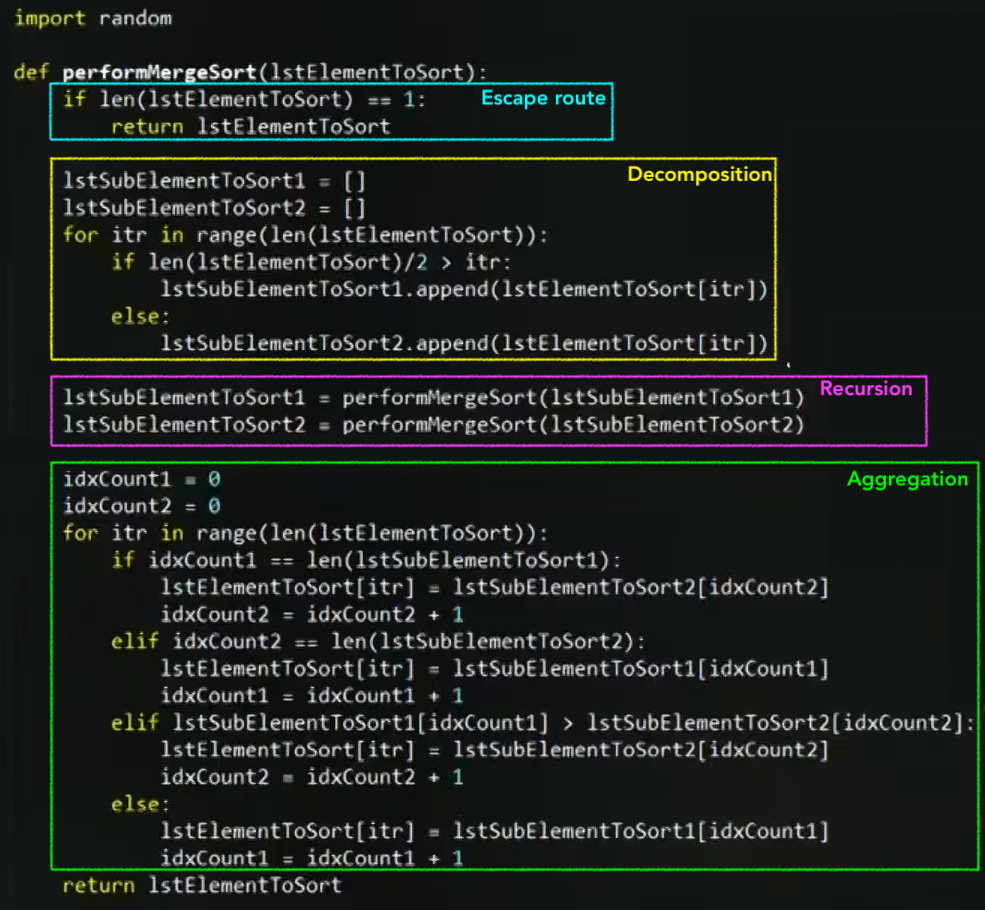
5-36screenshot

# Execution
1stRandom = []
for itr in range(0,10)
	1stRandom.append(random.randrange(0, 100))
print 1stRandom
1stRandom = performMergeSort(1stRandom)
print 1stRandom

Tim Sort

Tim Sort는 실세계의 data가 대략 정렬된 상태로 있는 경우가 많다는 경험에서 기반하여 디자인된 알고리즘

거의 다 정렬된 array에 대해서는 O(n)의 성능을 보임

부분적으로 정렬되있거나 정렬되어있지 않은 array에 대해서는 O(nlogn)의 성능을 보장함

Tim Sort는 Python의 list.sort() , 그리고 Java의 Array.sort(...) 중 argument가 object type일 때 내장 정렬함수로 쓰임
TimSort = Merge Sort + Insertion Sort

Merge Sort로 데이터를 나눈 후 각각에 작은 배열에 대해 Insertion Sort을 통해 정렬 시간을 줄일려는 생각을 하였음

run : run의 크기는 2^5개 또는 2^6개로 맞춰져야됨, 그리고 각 run들은 항상 정렬이 되있어야됨
TimSort 과정 :
1. 배열을 run으로 분할하기
  - 전체 배열에서 Binary Insertion Sort를 수행하여 정렬된 여러개 run들로 분할한다
2. 분할된 run을 병합하기
  
  [1] 병합되는 순서 :
  - 비슷한 크기의 run을 병합하기 위해서 다음 조건이 적용된 Stack이 활용됨
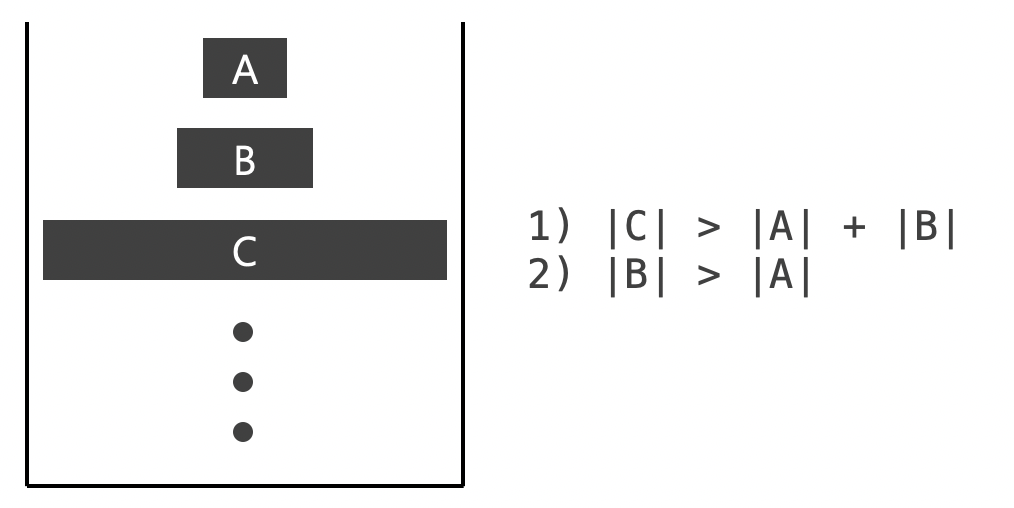
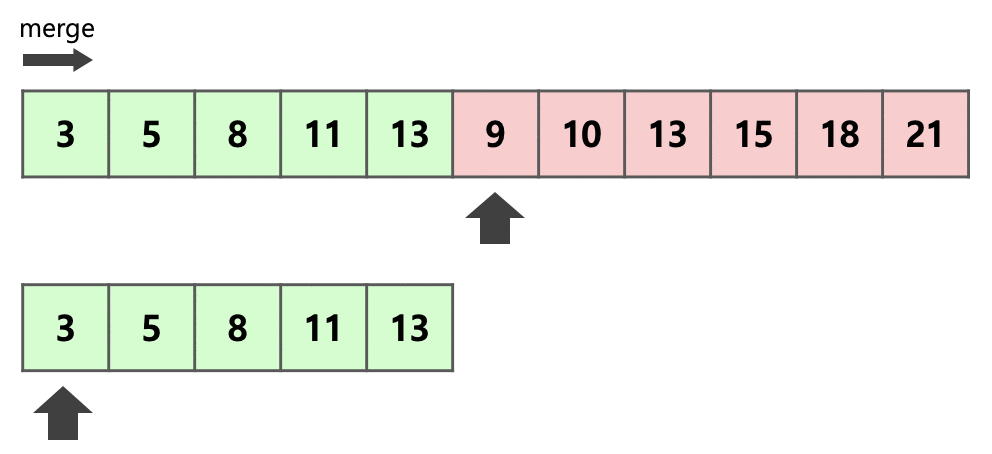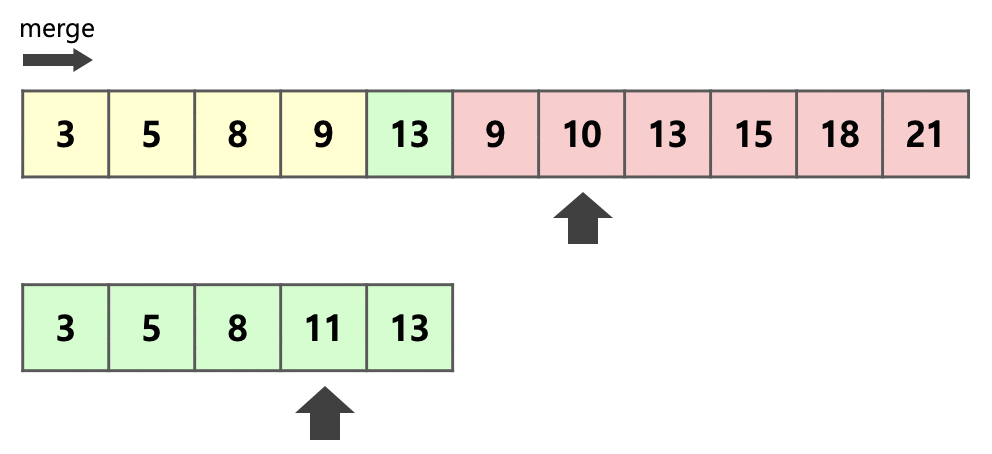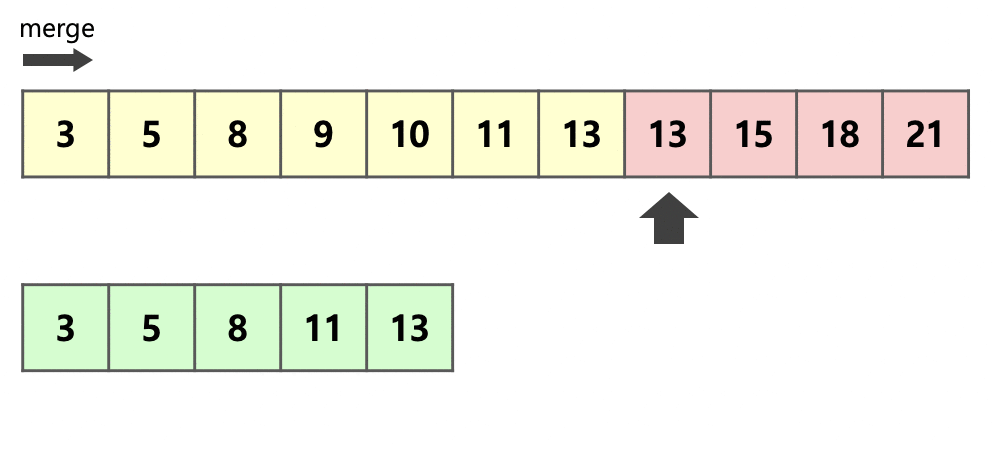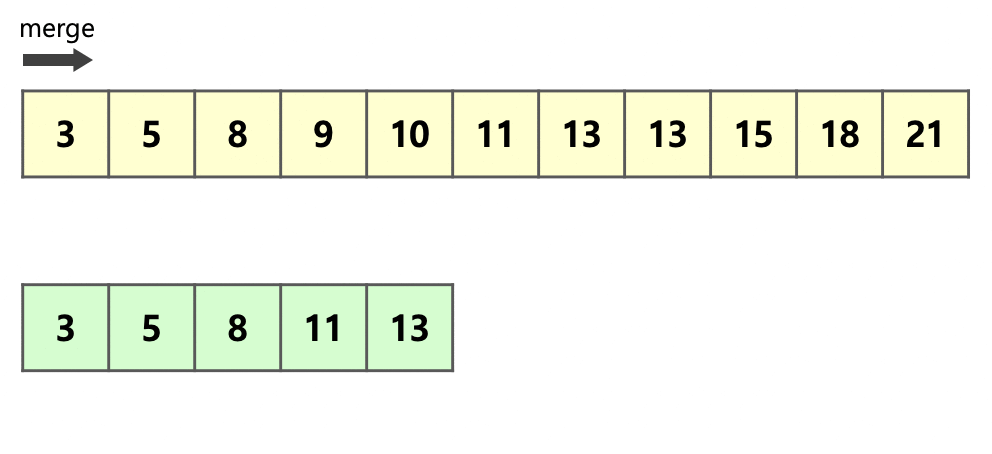
  [2] 2개 run이 병합될 때 적용되는 방법 :
  1. 메모리 사용량을 줄이기 위해서 run A와 B중 크기가 더 작은 A을 복사한다 (그림 : 밑에 array)
  2. run A와 B를 concat해서 run C가 생성된다 (그림 : 위에 array)
  3. 복사된 run A (그림 : 밑에 array)와 run B (그림 : 위에 array의 9부터 시작)를 순서대로 비교하면서 run C에 처음부터(그림 : 위에 array의 3부터 시작) 순서대로 적어넣는다
    - 최적화를 위해 복사된 run A와 run B를 비교하는 과정에서 Galloping mode가 적용됨

O(n) Sorting

비교 기반 접근법이 아님!

Counting Sort

조건 :
- Integers sequence 여 야됨 (Ranging from 0 to K)
각 숫자들이 몇번이나 일어나는지 count
- 즉, 비교가 필요없음!
만약 Input data array size가 n이고 Count array size가 R이라고 하면, n< R일 경우, time complexity를 O(R)이라고 나타낼 수 있음
- Example. [999999, 0] 배열을 정렬할 경우
- 왜냐하면 count array를 print하는 for문이 Input data array 를 count하는 for문 보다 iteration 수가 더 많기 때문에
정렬하려는 배열에서 동일한 값을 가지는 데이터가 여러 개 등장 할 때 효과적으로 사용할 수 있음

Radix Sort

1의 자리, 10의 자리, 100의 자리 … 순으로 값을 큐에 저장하고, FIFO로 출력하여 기존 배열에 덮어 쓴다
input array에 몇의 자리 숫자 까지 있는지 파악하는 방법 :
```
max = findMax(inputSeq)
digit = int(math.log10(max))
  
for iter in range(0,digit+1):
  # Placing values into buckets
  # Print the partially sorted values
```
Example. input array에서 젤 큰수가 30000 (max=30000) 일 경우

log10(30000) == log10(3 * 10^4) == log10(3) + log10(10^4) == log10(3) + 4 = 4.xxxx

digit == int(log10(30000)) == int(4.xxxx) == 4

Genetic algorithm

한 iteration 과정 : population selection cross over mutation new solution 생성완료 substitution
설정해야되는 parameter들 : iteration 횟수, population 크기

Graph

Terminology
- G = (vertex set, edge set)
- Adjacent vertex : 옆에 edge로 묶여있는 vertex
- Connected graph : if exist path from each to every other vertex
- Complete graph : if all vertex have path to every other vertex
- Directed Edge : 방향성이 있는 Edge
- Digraph = Directed Graph
- DAG = Directed Acyclic Graph
  - 사이클이 없는 Directed Graph
  - Tree structure로 변환하기 용이, 확률모델링에도 잘 활용할 수 있음
Storing Graph
- Directed Graph Density = Edge 갯수 / Vertex 갯수 (Vertex 갯수 - 1)
- Storing Vertex
  - Linked List, BST, Hash ..
- Storing Edges
  - 2 dimensional matrix
    
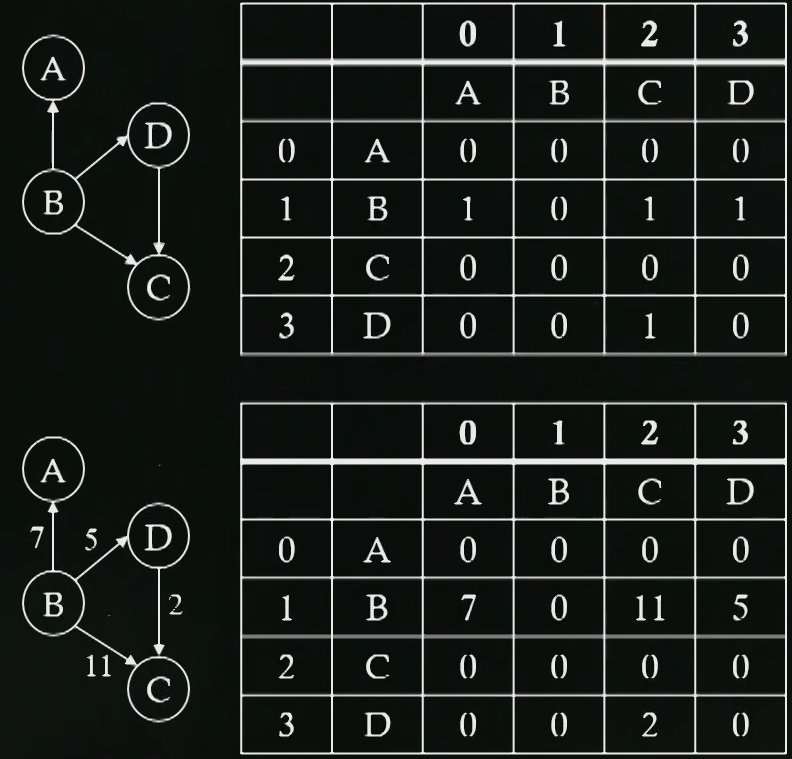
    더 많은 양의 데이터를 저장할 때 더 큰 공간이 필요로함
  - Adjacency list
    
    matrix를 활용할 경우 spase graph의 스토리지 낭비가 있음
    
    장점 : 스토리지 낭비를 줄일 수 있음
    
    단점 : Search time complexity가 matrix에 비해 늘어남
    - Linked list 말고 다른 데이터 구조(BST, Hash..)를 활용해서 어느정도 이 문제를 해결할 수 있음
Operations on Graphs
- Traverse (DFS vs BFS)
  - DFS : Pre-order를 자주 사용함, Stack or Recursion으로 구현
  - BFS : Level order traverse, Queue를 활용
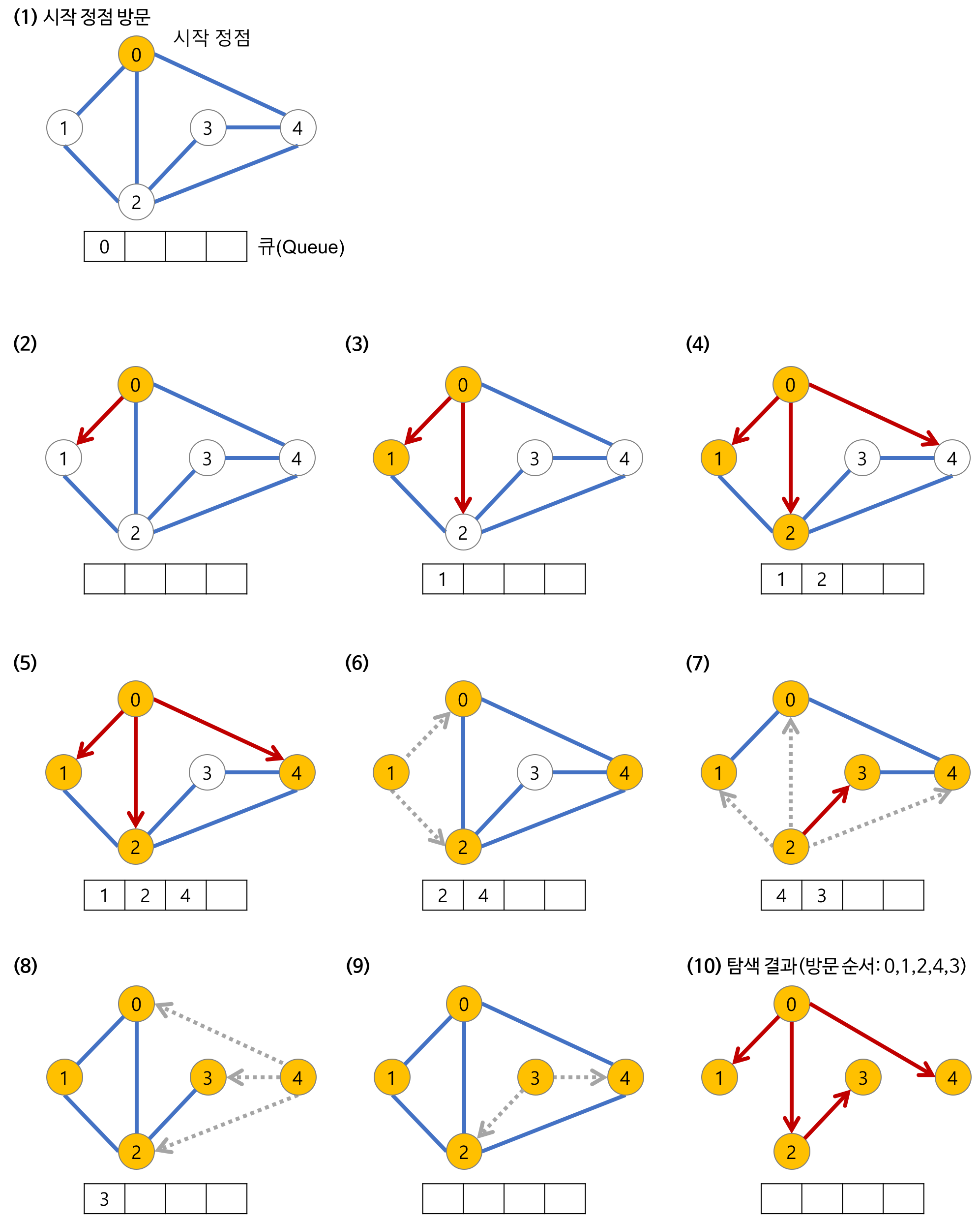
    - 参考： Blog
- 최단 경로 알고리즘
- - 우리의 destination까지 얼마나 걸릴 것인지 우린 알고싶음
  - Dijkstra’s Algorithm
    - 그래프 내 Edge의 가중치가 음수인 것이 하나라도 있다면 사용할 수가 없음
    - 다익스트라는 무향, 유향 그래프에서 모두 작동한다
    - 기본적으로 하나의 최단거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용
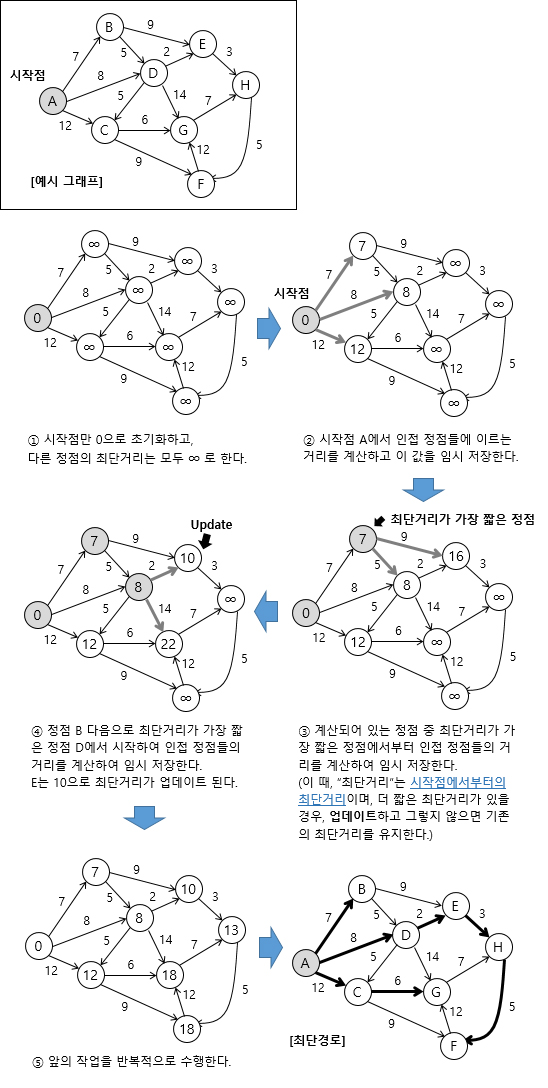
    - 최단거리는 여러개의 최단거리로 이루워져있음
      - A -> B -> C -> D 가 A에서 D로 가는 최단경로라면 그 과정 속에 있던 A -> B 그리고 B -> C 이 경로 또한 최단 경로가 되어야 함
      - 즉, 다익스트라 알고리즘은 작은 문제가 큰 문제속에 비슷한 형태로 포함되어있는 Dynamic Programming 유형
    - Time Complexity : O(Vertex 개수 ^2)
- Finding a set of path to control whole vertexes
  - Minimum spanning tree
  - 이 문제는 언제 활용될 수 있지?
    
    도로 건설 : 도시를 모두 연결하여 도로 길이 최소화
    
    전기 회로 : 단자를 모두 연결하여 전선 길이 최소화
    
    통신 : 전화선의 길이가 최소화하여 케이블망 구축
    
    배관 : 파이프를 모두 연결하여 총 길이를 최소화
    
    네트워크 : 라우터 경로 설정, 최적의 라우팅 경로 선택
  - Prim Algoritm
  - 无方向 그래프에서만 작동함
  - Logic :
    1. 임의의 노드를 선택하여 ‘연결된 NODE 집합’ 이라는 리스트에 삽입한다.
    2. 1단계에서 선택된 노드에 연결된 edge들을 ‘EDGE’ 리스트에 삽입한다
    3. ‘EDGE’ 리스트에서 최소 가중치를 가지는 간선부터 추출한다. (간선이 추가될 때마다 가중치를 기준으로 내림차순 정렬)
      - ‘EDGE’ 리스트에서 추출된 노드가 ‘연결된 노드 집합’ 리스트에 이미 존재한다면 스킵한다.(사이클 방지)
      - 반대로, 존재하지 않는다면 해당 노드의 간선정보를 ‘최소신장트리’에 삽입한다.
    4. 선택된 간선은 ‘EDGE’ 리스트에서 제거한다.
    5. ‘EDGE’ 리스트에 더 이상 간선이 없을 때까지 3, 4번 과정을 반복수행한다.
  - 예시 :
    
    아래 그림에서 파란색 요소들은 ‘연결된 노드 집합’에 삽입되었음을 의미한다
    
    아래 그림에서 빨간색 요소들은 ‘EDGE’ 리스트에 삽입되었음을 의미한다

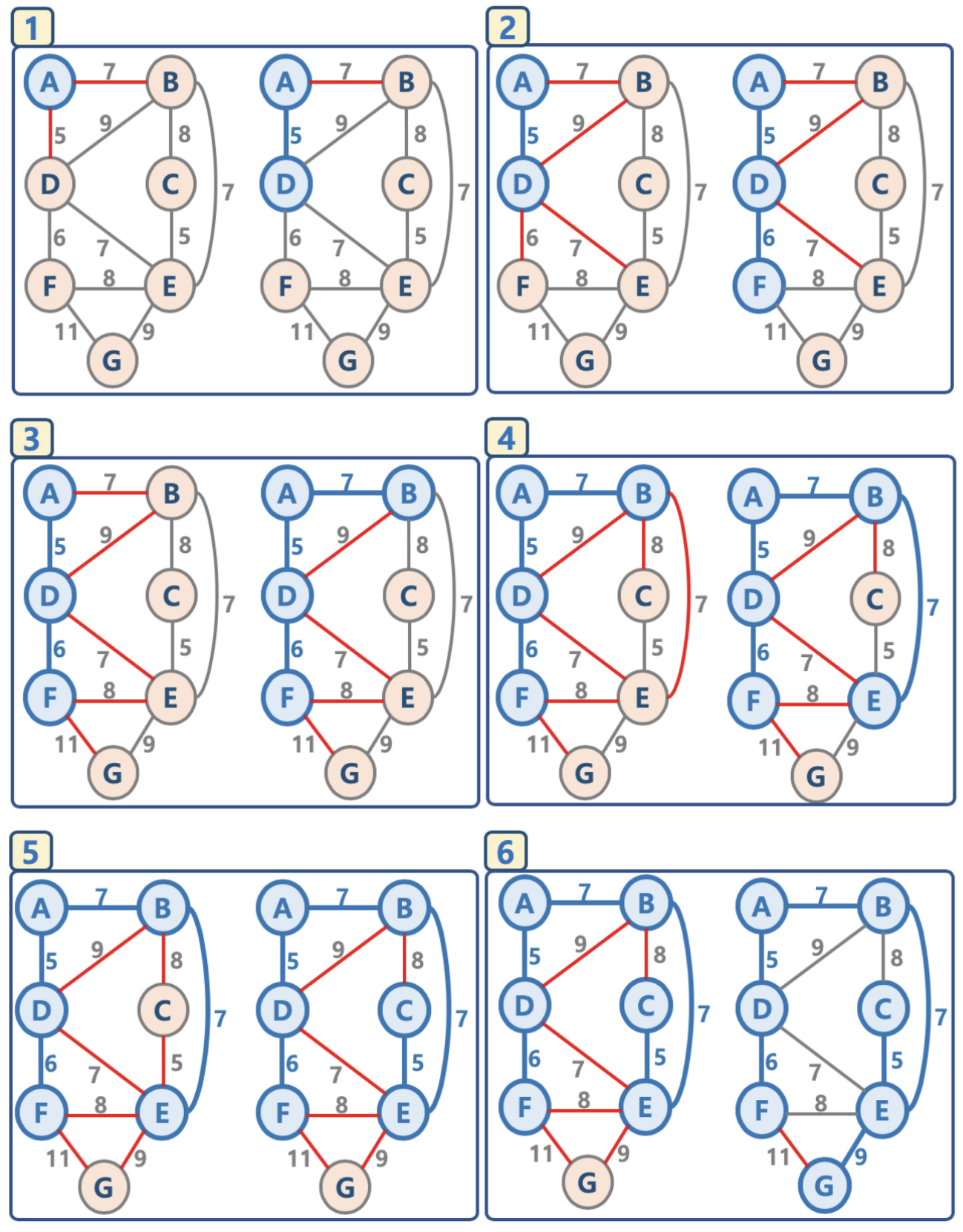
PREVIOUSUnion-Find

NEXT프로그램 언어에 적용된 데이터 구조들