01. CS231N 요약 (Background, Neural network)

Image

• 이미지는 숫자로 구성된 3D Array로 구성됨

  

  • 숫자 = 0~255
  • 3D Array = [Hight] × [Width] × [Color channel]

Challenges

1. 보는 시각에 따라 이미지는 다르게 보일 수 있음
2. 조명의 밝기/색상에 따라 다르게 보일 수 있음
3. 인식하려고하는 대상이 항상 정면을 서있는게 아님. 비틀어져있고 회전해있고 누워있고
4. 인식대상이 은폐엄폐/가려짐 등으로 일부만 인식 가능
5. 배경혼란, 인식대상물과 배경의 패턴이 비슷
6. 동종 내 다양성, 같은 고양이라도 페르시아고양이, 길고양이 다 다르게생김

Challenges 접근 방법

1. 이미지의 특징 파악
   • 특징적인 엣지나 모형을 찾아서 Library화 시킴 그리고 배열 상태 비교 후 Classification 함
   • 성능이 낮음

2. 데이터 기반 접근

   • 이미지와 레이블로 구성된 데이터셋을 수집

   • 데이터셋에 대해서 이미지 Classifier를 학습시킴

     def train(train_images, train_labels):
       ...
       return model
     

   • Test 이미지셋들에 대해서 학습시킨 이미지 Classifier를 평가

     def predict(model, test_images):
       ...
       return test_labels
     

Nearest Neighbor Classifier

• Training 단계 :
  • 모든 학습 데이터들을 메모리 상에 올려서 기억하게 됨
• 예측 단계 :
  • Test 이미지 한장을 L1 Distance를 사용하여 모든 학습 데이터들과 비교
  • L1 Distance 값이 가장 작은 학습 데이터를 찾아 Test 이미지의 레이블을 예측할 수 있음
• 단점 :
  • 학습데이터 양에 따라 Classification 작업 (예측 단계) 시간이 선형적으로 증가하게됨
  • 속도를 빨리할 수 있는 Nearest Neighbor Classifier들 : ANN, FLANN

K-Nearest Neighbor Classifier

• K개의 근접한 학습데이터를 찾는 방식

• 보통 1-Nearest Neighbor보다 성능이 좀 더 좋음
• 근데 현실에서는 사용해서는 안됨

Linear Classification (Score function)

• 이미지 내의 모든 Pixel값 들에 대해서 Weight를 곱하여서 처리 한 것의 “합”이다

  

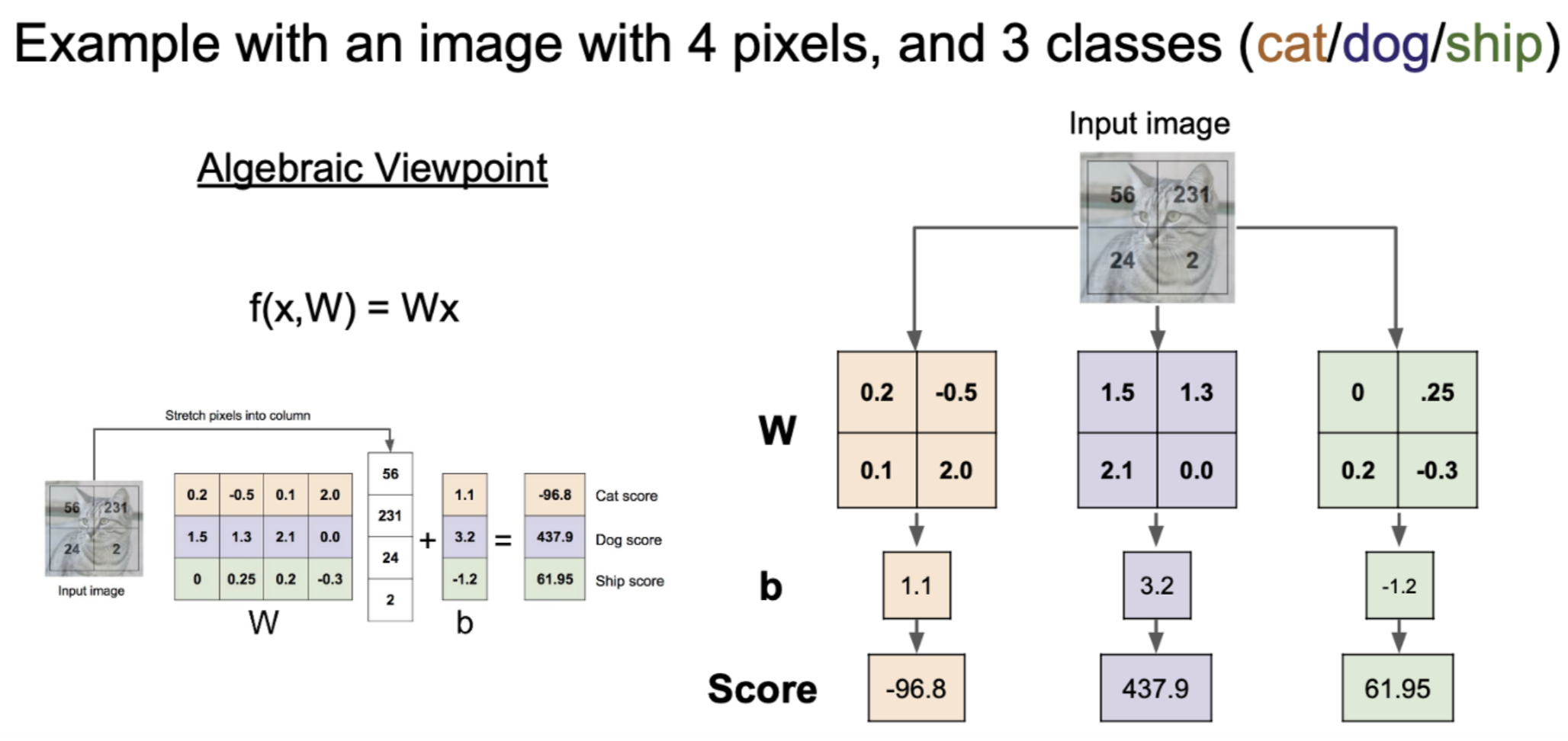
  • Linear Classification를 통해 입력 이미지의 각 class에 대한 score를 낼 수 있음

Loss Function

• Linear Classification를 통해 나온 score들이 어느 정도 좋거나 또는 나쁘냐의 정도를 정량화 하는 것

• Example 1) SVM Hinge loss

  """
  SVM 의 Hinge Loss를 사용하여 Loss 값 구하기
  x : Input image
  y : Input image label
  W : Score function's Weight
  """
  def Li_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores-scores[y]+1) 
    margins[y] = 0
    loss_i = np.sum(margins) # np.mean을 써도 큰 의미는 없음, 단지 scale만 작아짐 
    return loss_i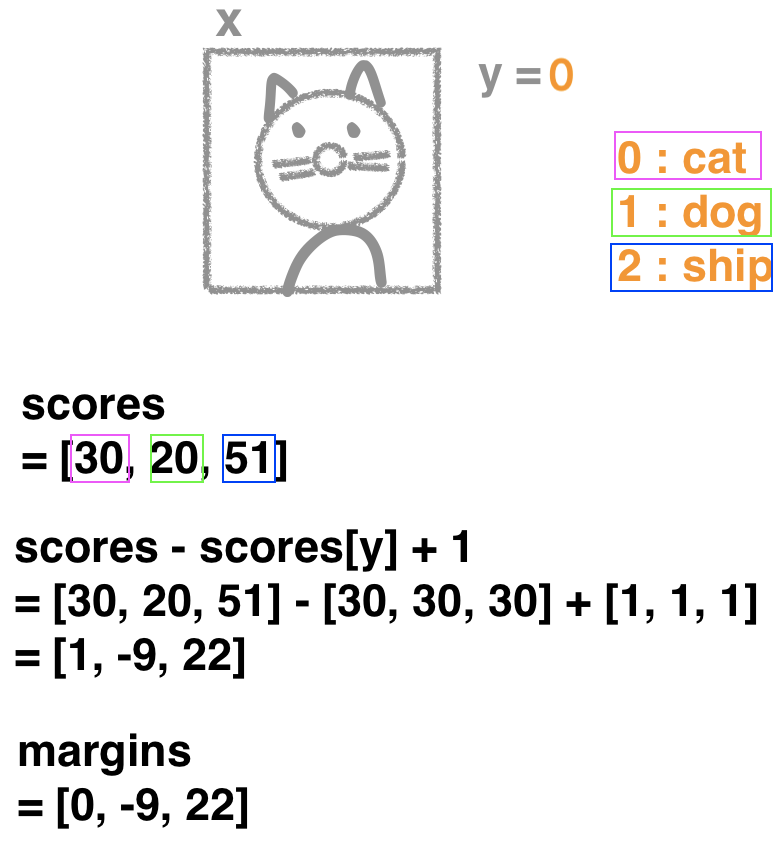
  

  

  • Li_vectorized(x, y, W) return값 최소/최대 = 0 / ∞ （则, Loss值为’0’ 表示最好）

  • 특성 : 미세한 데이터 변경에 둔한 편, 단지 정답 class가 다른 class보다 높냐에 초점을 둠

• Example 2) Softmax Cross entropy loss

  • Softmax function : Score function을 통해 나온 score vector의 각 element값들 0~1사이로 변경

    • 변경된 element값들의 총 합은 1

    import numpy as np
    # Score function을 통해 나온 score vector
    f = np.array([3.2, 5.1, -1.7]) 
    # Numeric problem를 방지하기 위해 
    f = f - np.max(f)
    # Softmax function
    p = np.exp(f) / np.sum(np.exp(f))
        
    '''
    f == [-1.9  0.  -6.8]
    p == [0.12998254 0.86904954 0.00096793]
    '''
    

  • Cross entropy loss

    

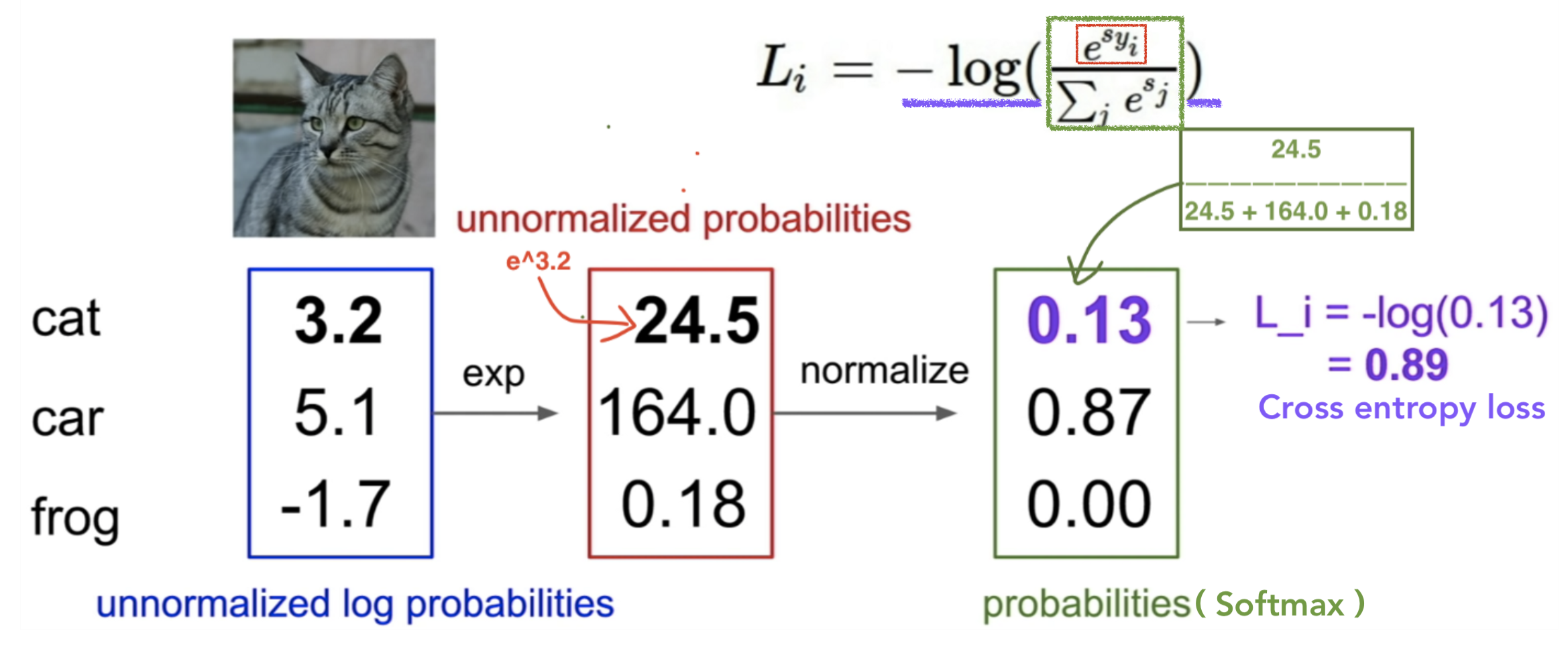
    CrossEntropyLoss = -np.log10(p)
    '''
    CrossEntropyLoss == [0.88611498 0.06095547 3.01415795]
    '''
    

    • CrossEntropyLoss 의 최소/최대값 : 1 / ∞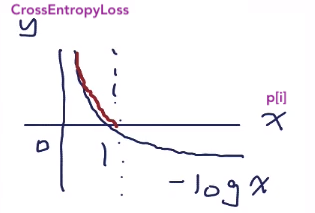

      

      (즉, score를 잘 맞추면 loss는 0에 가까움 , 잘 못 맞추었다면 loss는 ∞에 가까움)

    • 특성 : SVM에 비해 미세한 데이터 변경에 확실히 예민하고 loss값에 변동이 있음

Weight Regularization

• 0이라는 loss값을 만드는 weight가 유일하지 않음

• 유일한 weight값을 결정해주기 위해서 Regularization를 도입

  

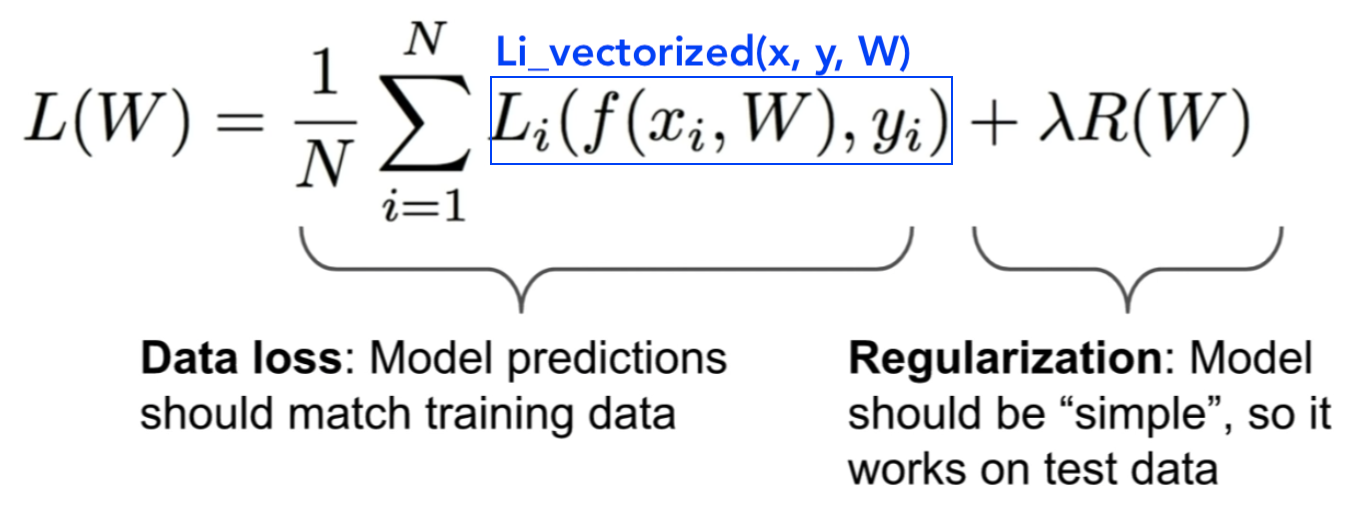
  • Data Loss : 학습용 데이터들에 최대한 최적화를 하려고 노력함

    • Classifier 다항식 차수가 깊어지게됨

  • Regularization : 테스트 데이터들에 최대한 일반화를 하려고 노력함

    • Classifier 다항식 차수가 깊어지지 않도록 방지함
    • λ : Regularization 적용 가중치

  • Data Loss 과 Regularization가 서로 싸우며 결국 가장 최적화된 weight값을 추출하게 됨

  • Ex) L2 Regularization

    

    • L2 Regularization 경우, 한쪽으로 쏠리기 보다는 서로 비슷하게 spread out된 Weight 벡터를 선호

      Classifier 다항식의 전체 차수를 0에 가깝도록 유도

    • L1 Regularization 경우, 한쪽으로 쏠려 있고 나머지는 0이 되는 sparse한 Weight 벡터를 선호

      Classifier 다항식의 특정 원하는 차수를 0이 되도록 만듬

Optimization

• Loss를 minimize하는 weight를 찾아가는 과정

• Gradient descent : 경사를 따라서 조금씩 내려가는 방식으로 weight를 업데이트함

  # Full-batch gradient descent : 훈련데이터 전체를 활용
  while True :
    weight_gradient = evaluate_gradient(loss_func, data, weight)
    weight = weight - learning_rate * weight_gradient # weight 업데이트
  

  # Mini-batch gradient descent : 훈련데이터의 일부만을 활용 (성능을 높임)
  while True:
    data_batch = sample_training_data(data, 256) # sample 256 examples
    weight_gradient = evaluate_gradient(loss_fun, data_batch, weights)
    weight = weight - learning_rate * weight_gradient # weight 업데이트
  

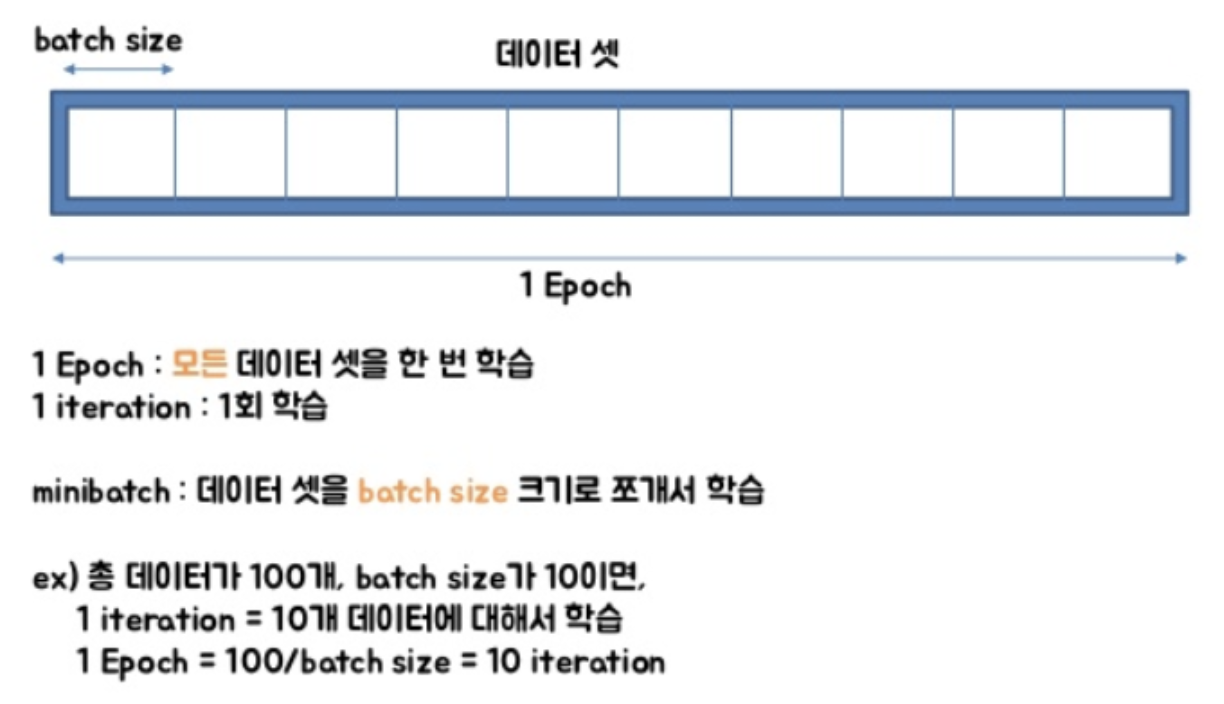
  • Mini-batch size : CPU/GPU 환경에 따라 설정함

  • Weight를 업데이트하는 또 다른 방법들 :

    • momentum : loss 가 줄어드는 속도까지 고려, 더 빠른 효과가 있음

    • Adagrad

    • RMSProp

    • Adam

      …

Backpropagation

• Computational graph를 이용해서 함수를 표현하게 되면, 모든 변수에 대해서 재귀적으로 gradient를 계산하는 backpropagation을 사용할 수 있게 됨

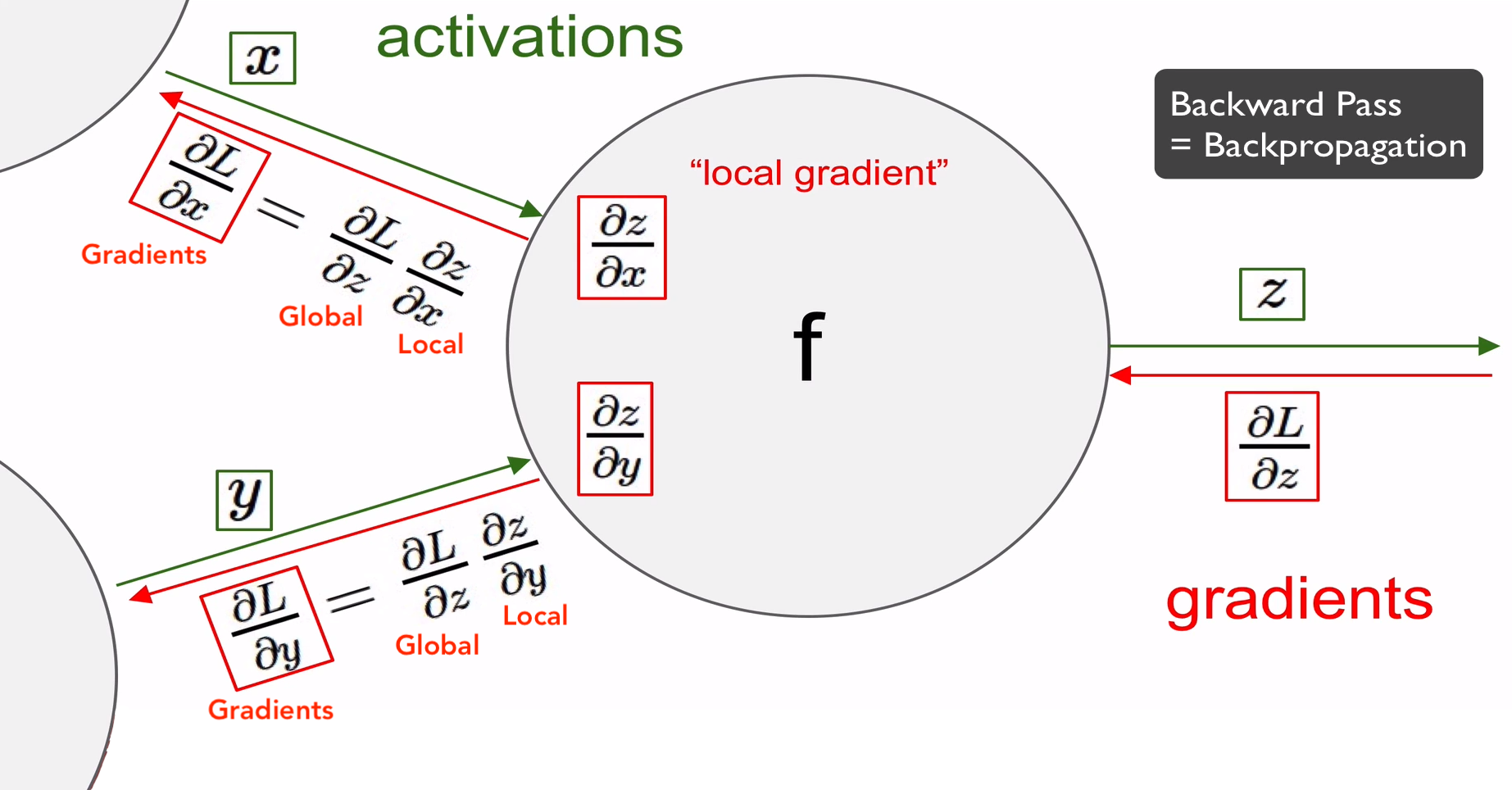
• Local Gradiant : Forward pass 할 때 구해서 메모리에 저장해 둔다

• Global Gradiant : Backward pass 할 때 구함

• Gradiant = Local Gradiant × Global Gradiant

• Example

  

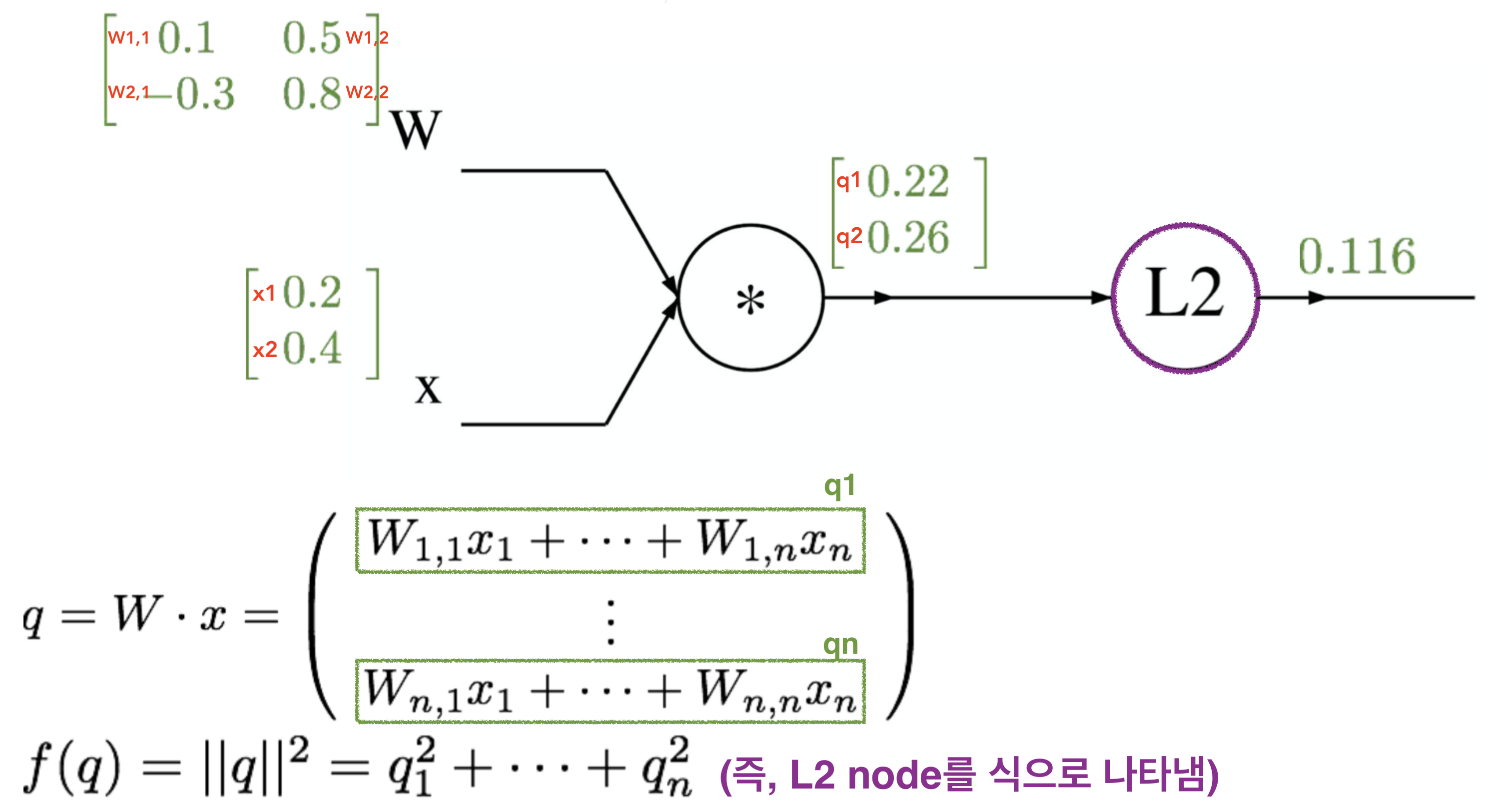
  • Backward pass 하면서 gradient 계산

  

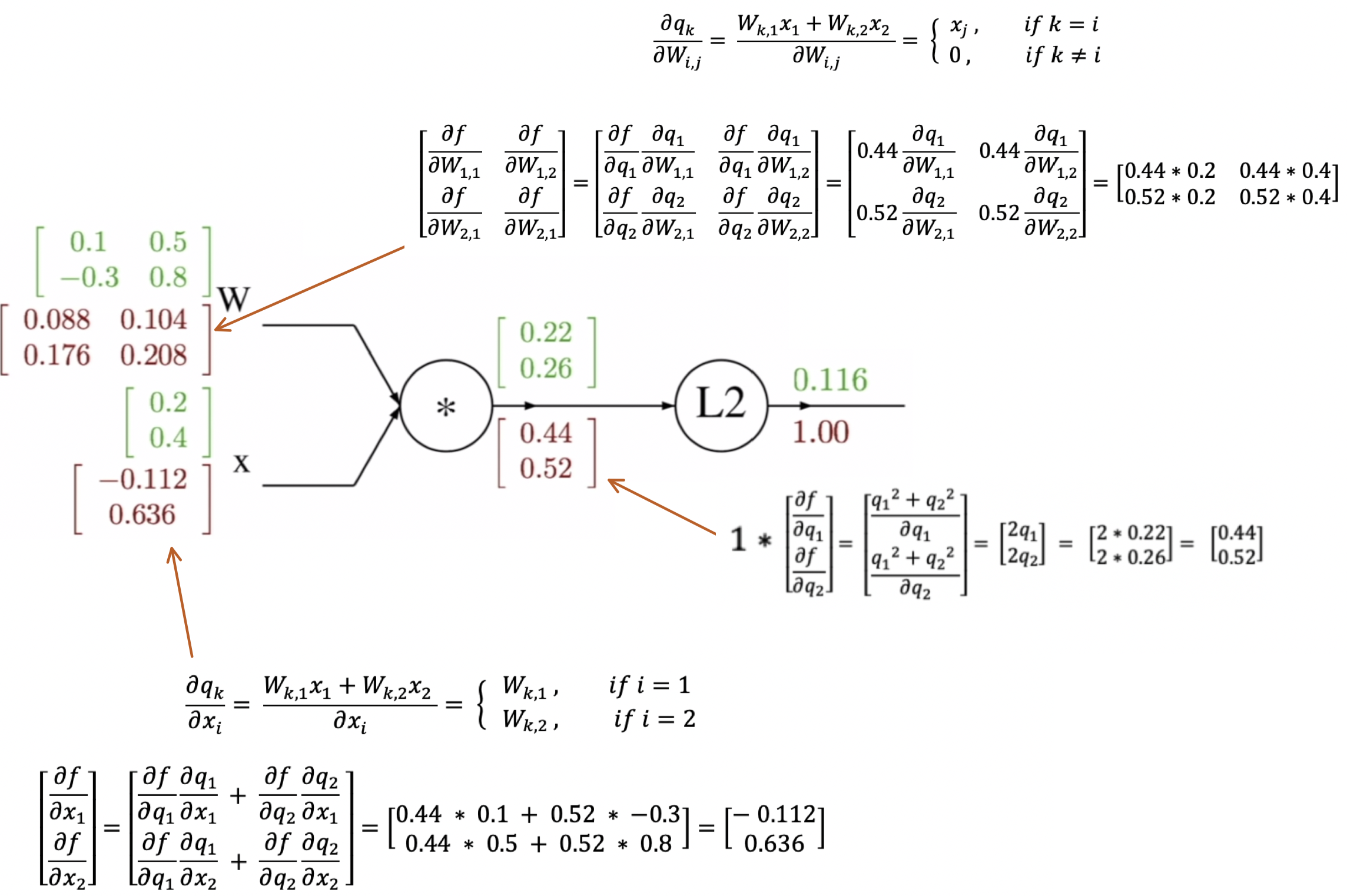
Neural Network

Neuron

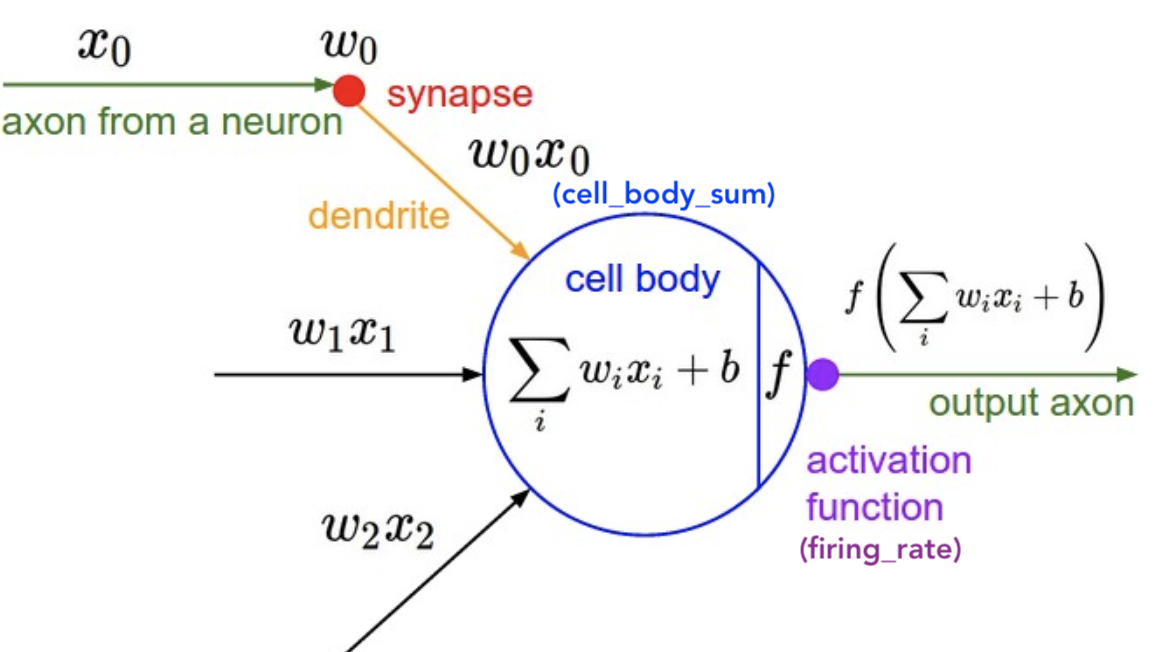
class Neuron(object):
  # ... 
  def forward(self, inputs):
    """ assume inputs and weights are 1-D numpy arrays and bias is a number """
    cell_body_sum = np.sum(inputs * self.weights) + self.bias
    firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
    return firing_rate

Architectures

• Fully Connected Layers : 모든 node (or Neuron)들이 연결 되어있다

• Example : 3-Layer Neural Network (or 2-Hidden-Layer Neural Network)

  

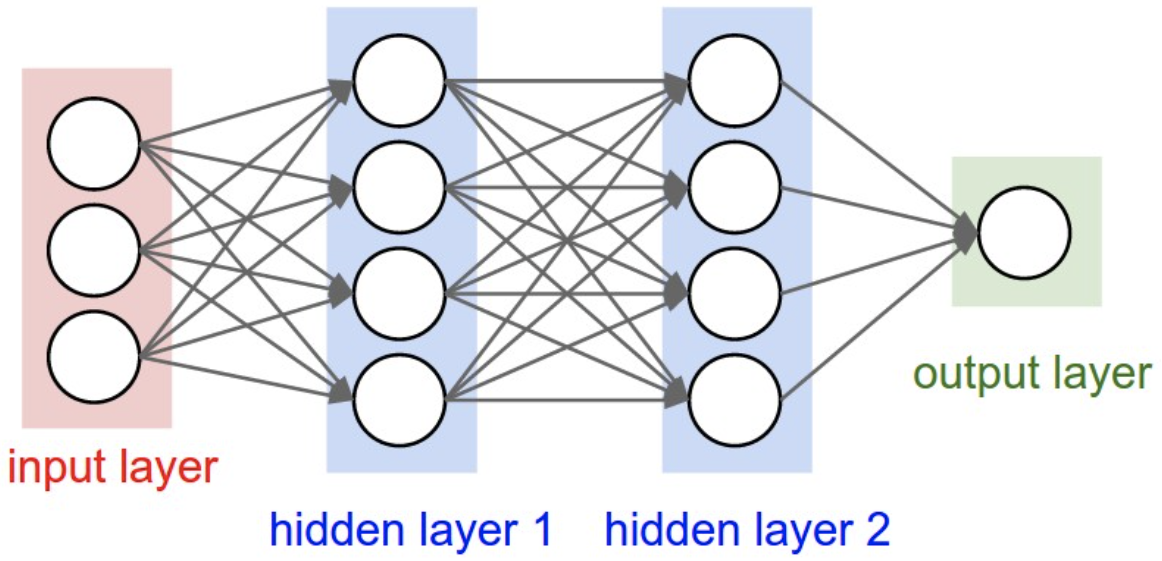
  # forward-pass of a 3-layer neural network:
  f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
  x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
  h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
  h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
  out = np.dot(W3, h2) + b3 # output neuron (1x1)
  

• 데이터의 Overfitting이 일어나지 않도록, Neural Network를 구성하는 방법은 Network를 작게 만드는게 아니라 Regularization Strength(λ)를 더 높혀줘야된다

• 그래서 Neural Network는 Regularization 를 잘 한다는 전제 하에 network가 더 크면 클 수록 좋다

Activation Function

• 활성화(Activate)라는 이름에서 알 수 있듯이 활성화 함수란 입력 신호의 총합 cell_body_sum 이 활성화를 일으키는지 정하는 역할을 한다

• Activation Function를 왜 반드시 이용해야되나?

  • Activation Function를 사용하지 않으면 Neural Network 전체가 몇개의 Layer를 가지든 간에 단일의 linear classifier 수준이 되버림

  • Example : y=ax를 Activation Function으로 사용하게 된다면

    • 2계층 layer일 경우 y=a(ax), 3계층 layer일 경우 y=a(a(ax)) … n계층 layer일 경우 y=(a^n)x

• 종류들 :

  

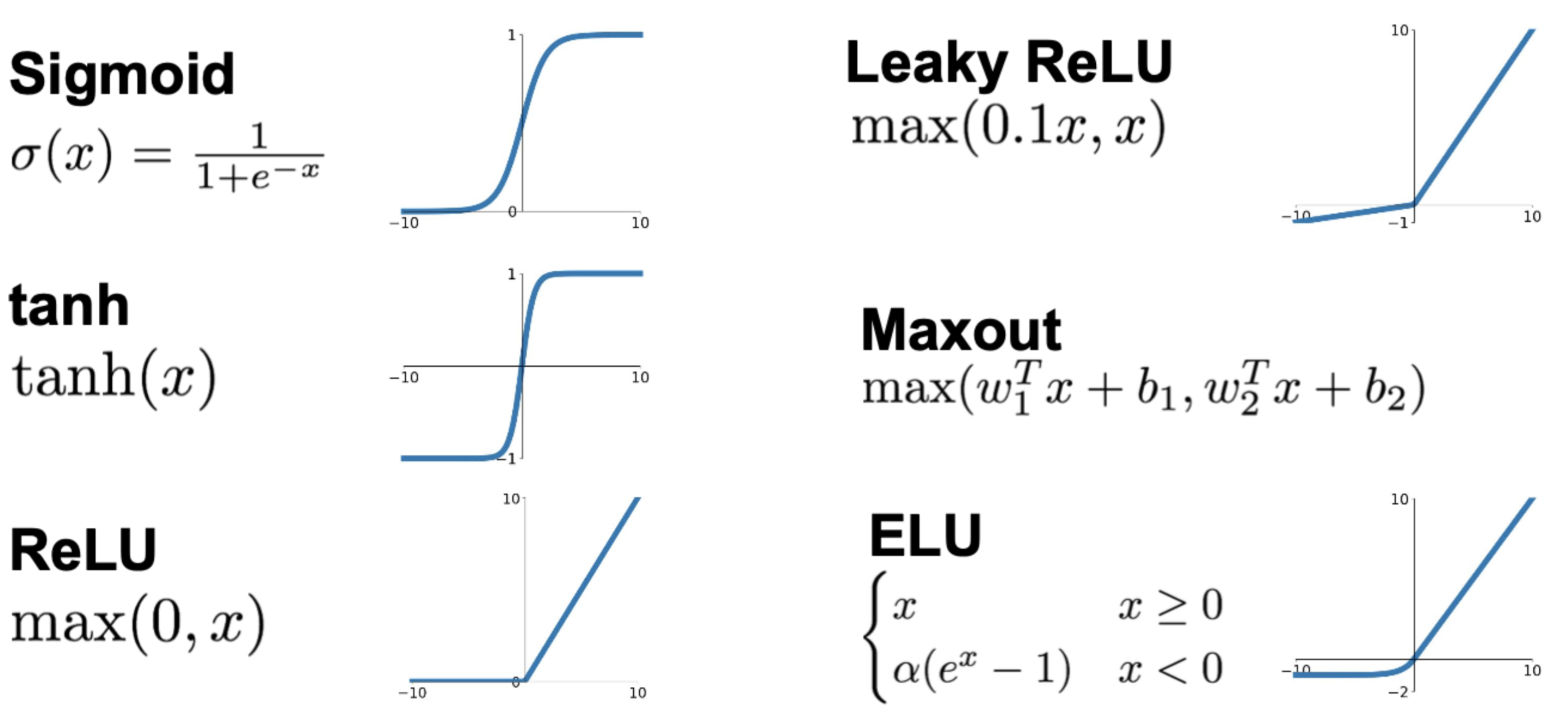
  • 다른 뉴런에게 자극을 보낼지, 아닐지를 결정하는 게 Neural network에서의 Activation function과 같으며, 실제 뉴런과 가장 비슷한 기능을 수행하는 것은 바로 ReLU

  • Sigmoid

    • 넓은 범위의 숫자를 [0,1]사이로 squash 해줌

    • 요즘 거의 잘 사용되지 않음

    • 문제점 :

      1. Vanishing gradient

         

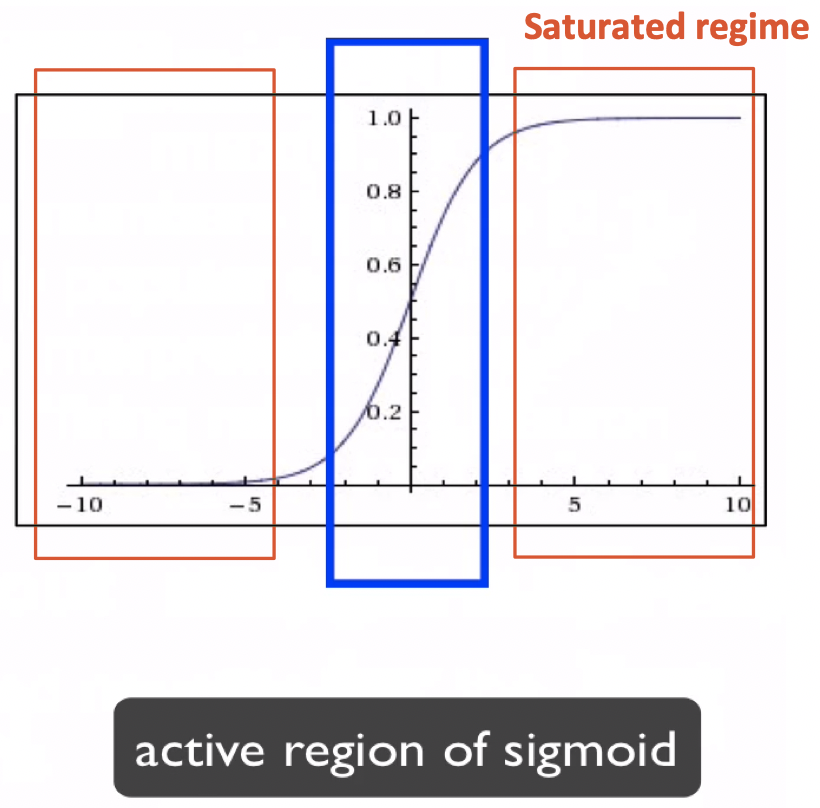
         Active region of sigmoid : sigmoid가 실제로 Active하게 역활할 수 있는 부분

         Saturated regime : local gradient가 0을 가져 backpropagation이 멈추게됨

      2. Not zero-centered (모든 y값이 0 이상임)

         zig zag 방식으로 이동하게되서 결과적으로 매우 느리게 수렴됨 – 최적의 weight를 찾는게 느림

      3. Exp( ) 연산적으로 hight cost

  • Hyperbolic Tangent (tanh)

    • 넓은 범위의 숫자를 [-1,1]사이로 squash 해줌
    • Zero-centered (y값의 중간값이 0임)
    • 문제점 :
      1. 여전히 Saturated regime 이 존재함

  • Rectified Linear Unit (ReLU)

    • x가 positive인 지역 (그래프 제1사분면)에선 Saturated regime 가 존재하지
    • 연산이 매우 효율적
    • Sigmoid/tanh에 비해 6배 이상 빠르게 수렴 – 최적의 weight를 찾는게 비교적 빠름
    • 문제점 :
      1. Not zero-centered
      2. x가 0보다 적은 지역은 gradient가 0이 되서 Vanishing gradient가 발생

  • Leaky ReLU

    • ReLU와는 다르게 x가 0보다 적은 지역에도 gradient를 가질 수 있음

      즉, backpropagation이 멈출일이 없음

  • Exponential Linear Units (ELU)

    • ReLU 장점들을 다 가지고 있으면서 gradient가 죽지 않음
    • Zero mean output에 가까운 형태를 가짐
    • 문제점
      1. Exp( ) 연산적으로 hight cost

  • Maxout Neuron

    • 입력 x를 받아드리는 특정한 기본 함수를 미리 정의하지 않음
    • gradient가 0이 되지도 않고 backpropagation이 멈추지도 않음
    • 문제점 :
      1. 뉴런 마다 두개의 parameter를 가지고 있기 때문에 연산이 두배로 증가

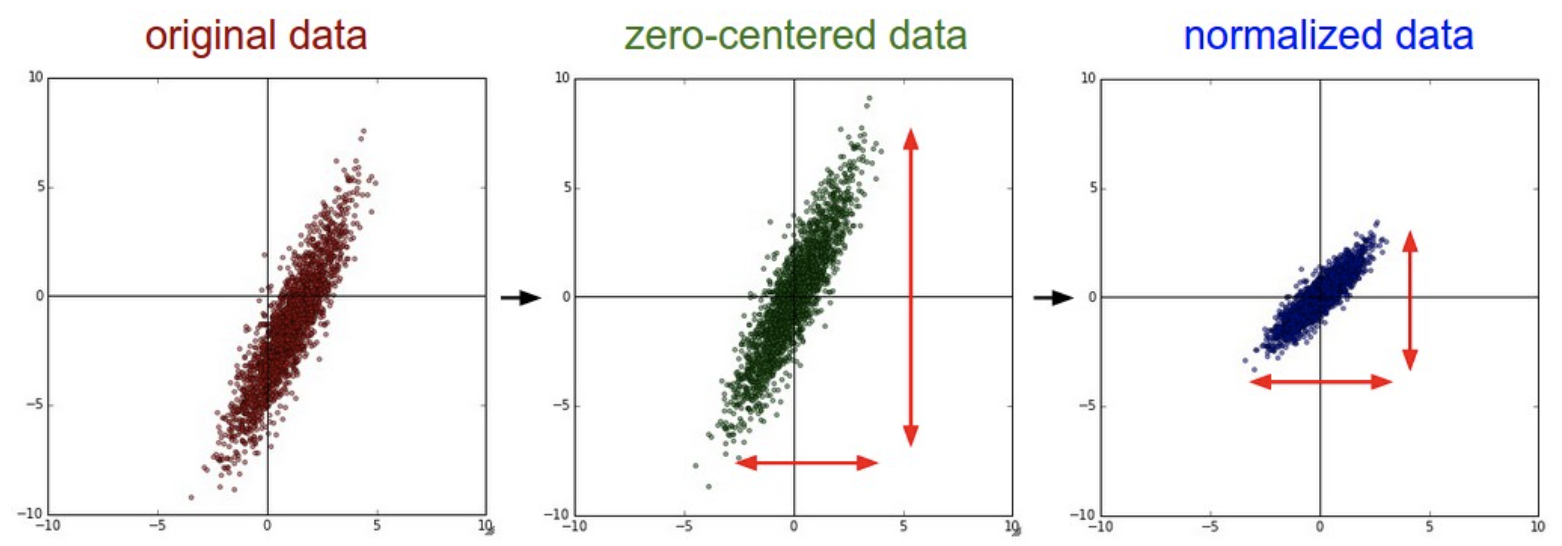
Data Preprocessing

• Zero-centered :

  • 각 데이터에 평균을 빼줌

    original_data = original_data - np.mean(original_data, axis = 0)

    ⚠️ 参考 ： 이 전처리 방법은 Sigmoid의 Not zero-centered 문제를 해결하기엔 충분하지 못함

    • 처음에 input 이미지가 Zero-centered로 전처리되면 1번째 layer는 해결이 될 수 있겠지만 그 다음 layer부터 다시 문제가 반복됨

• Normalized data : 특정 범위안에 데이터가 들어갈 수 있게 만들기

  • 각 데이터에 표준편차를 나눠줌

    original_data = original_data / np.std(original_data, axis = 0)

  • 이미지에서는 일반적으로 Zero-centered는 수행하지만 Normalization는 수행 안함

    👉 이미지의 각 pixel는 이미 0~255 사이에 값을 가지고 있으니깐

Weight Initialization

방법0. 모든 initial weight를 0으로 설정

• 모든 Neuron들은 다 같은 연산을 수행함 – 결국, 모든 Neuron들이 모두 똑같이 생기게 된다

방법1. Small random numbers

• 표준정규분포에서 샘플링하는 방법을 사용한 다음 더 작을 값을 위해 스케일링 해줌 (0.01를 곱해줌)

  W = 0.01* np.random.randn(fan_in, fan_out)

  • fan_in : number of inputs
  • fan_out : number of outputs

• Network가 작은 경우에 문제 없음, 하지만 Network가 큰 경우 문제가 생김

  • 모든 Activaton들이 0이 되버림
  • Backward pass를 하게된다면 Vanishing gradient가 발생하게 됨
  • 만약 W = 0.1* np.random.randn(fan_in, fan_out) 일 경우
    • 거의 모든 Neuron들이 -1 또는 1로 Saturation 됨
    • Gradient들도 모두 0이되서 weight 업데이트가 일어나지 않음
  • 즉, 스케일링이 너무 작으면( × 0.01) 사라져버리고 너무 크면 ( × 0.1) Saturation 됨

방법2. Xavier Initialization

• input의 개수가 많으면 weight값이 작아지고 input의 개수가 적으면 weight값이 커지는 방식으로 진행하는 방식

  W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)

• 하지만 Linear activation이 있다는 가정하에 잘 작동함

  • ReLU (Non-linear형) 를 쓰면 잘 작동하지 못함
  • ReLU는 출력의 절반을 죽이고 그 절반은 매번 0이 되기 때문에 출력의 분산을 반토막 내버림

방법3. He at al., 2015

• Activation function이 ReLU일 경우 최적인 weight 초기화 방법

  W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in/2)

  • Neuron들 중 절반이 없어진다는 사실을 고려해서 2로 나눠줌

방법4. Batch Normalization

• Batch :

  

• 각 layer들을 거치면서 입력값의 분포가 달라지는 현상이 발생하기 때문에 학습 불안정화가 생긴다고 주장

  

• batch normalization은 학습 과정에서 각batch 단위 별로 데이터가 다양한 분포를 가지더라도 각 batch별로 평균과 분산을 이용해 정규화 시켜줌

  

• Batch-Norm은 입력의 스케일만 살짝 조정해주는 역할이기 때문에 Fully-connected 와 Conv Layer 어디에든 적용할 수 있음

  

  • Conv Layer의 경우, Activation map(채널, Depth)마다 평균과 분산을 하나만 구함. 그리고 현재 Batch에 있는 모든 데이터로 Normalize 해줌. (Conv Layer 출력인 activation maps이 ‘공간적 구조’를 유지하고 있기를 원하기 때문에 이 점을 고려해서 CNN Activation Map을 Normalize 할 때는 전체 map의 평균과 분산을 같이 구함)

  

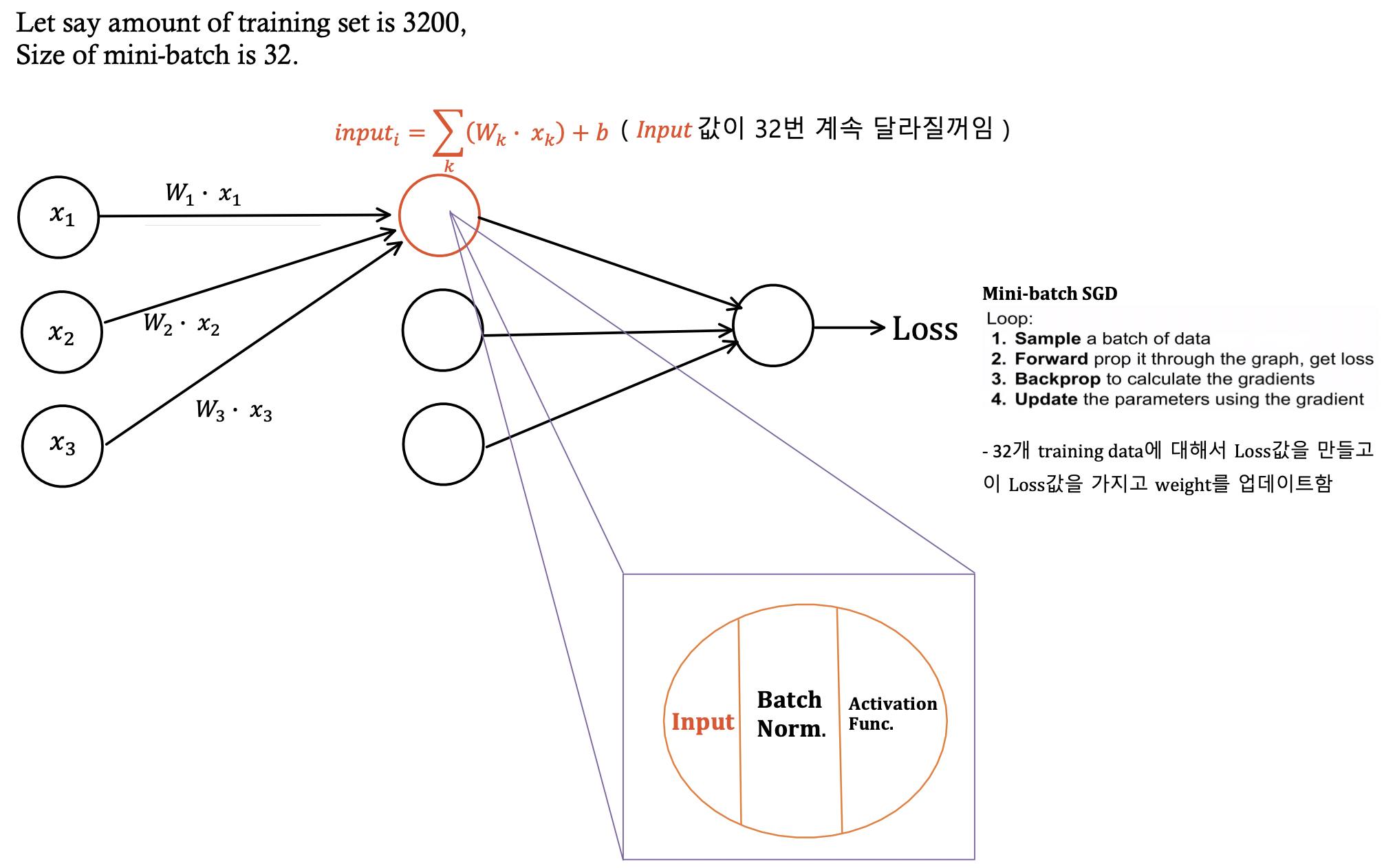
  • Batch 사이즈가 작으면 정확도가 떨어지긴 하겠지만 여전히 비슷한 효과를 줄 수 있음

  

  • 4번 단계에서 Unit gaussian으로 normalize 된 값들을 감마로는 스케일링 효과를 베타는 이동의 효과를 줄 수 있음
    • 추가적인 유연성을 제공

• 장점 :

  • Learning rate가 다소 큰 값을 가지더라도 그걸 허용해줌으로써 빠른 학습을 가능케 하는 효과가 있음
  • weight 초기화에 너무 의존하지 않아도 됨

• Batch Norm이 regularization의 역할도 함

  • 각 Layer의 출력은 해당 데이터 하나뿐만 아니라 batch안에 존재하는 모든 데이터들에 영향을 받음 (평균, 분산)

    (왜냐하면 각 레이어의 입력은 해당 배치의 (표본) 평균으로 Normalize 되기 때문)

• Batch Normalization를 사용하면 Dropout을 사용할 필요가 없다고 함

Training (Transfer Learning)

• 우리 모델을 처음부터 학습시키는 경우는 잘 없다

• 이미 연관된 다른 데이터셋으로 학습된 모델의 Weight들을 가져와서 이 가중치를 우리의 데이터에 적용시키는 방법 :

  • Small size dataset 일 경우 :

    

    • 즉, fix한 부분은 feature를 추출해주는 역할로 사용하면됨

  • Medium size dataset 일 경우 :

    

    Tip : top layer들의 경우 learning rate설정을 원래의 learning rate의 약 1/10을 사용하고 중간 layer들의 경우 learning rate설정을 원래의 learning rate의 약 1/100을 사용을 추천

• 이런 pre-trained 모델을 활용하여 학습하는 방식이 처음부터 학습을 시키는 방식보다 성능이 잘나오는 이유 :

  • pre-trained 모델이 ImageNet 데이터셋으로 훈련된 것이라 하면..

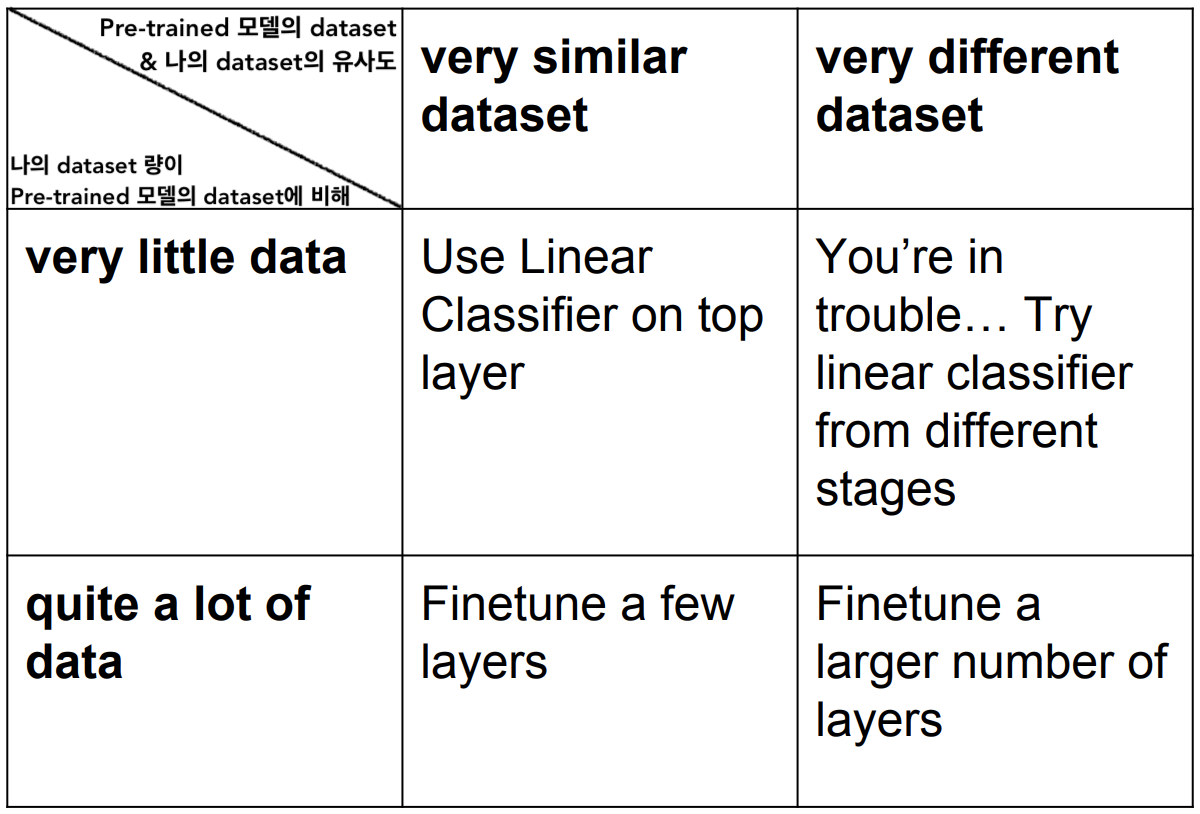
    1. ImageNet 데이터셋과 유사한 이미지들을 classify 해야될 경우, top layer들만 학습시켜도 좋은 성과를 얻을 수 있음
    2. ImageNet 데이터셋과 관련없는 데이터셋 (ex. 의료 데이터) 을 classify 해야될 경우, 학습 시켜야되는 layer를 top layer들 부터 중간 layer들 까지 올려야됨

    🤔 그럼 중간 layer들 에 전혀관계 없는 이미지 (ex. 의료 데이터)에 대해서 학습을 시켰다고 해서 어떻게 의료 데이터에 대한 classify 성능이 더 좋아지냐?

    • 가장 앞단의 filter에서는 Low level의 feature들(edge, color 등)을 인식하고 뒷쪽으로 갈 수록 앞쪽 layer의 filter들과 합성되어서 점점 abstract한 것들을 인식함.

      

      그래서 Low level의 feature를 미리 학습해 놓는다는 거는 그 어떤 이미지를 분석 할 때도 도움이 됨

• 정리를 해보면 :

  

Babysitting the Learning Process

• Learning 과정을 어떻게 관리하고 시작해 나가야되는지?

  1. 전처리
     • 이미지에 대해선 Zero-centered 수행
  2. Neural Network Architecture 결정
     • Hidden Layer는 몇개를 둘 것인지? 각각의 Layer에는 몇개의 Node를 둘 것 인지?

  3. Loss값 체크 (Sanity Check)

  4. 일부 training set을 활용하여 모델을 훈련시켜 Overfitting 일어나는 확인

     • Overfitting : 최종적으로 Loss 값이 거의 0에 가깝게 매우 작고 training set과 validation set에 대한 accuracy는 1일 경우

     • 모델이 Overfitting이 일어났다면, 즉

       💁🏻 Backpropergation이 동작을 잘하고 있는 걸 알 수 있음

       💁🏻 Weight 업데이트도 제대로 동작하고 있는 걸 알 수 있음

       💁🏻 Learning rate도 크게 문제가 없다는 걸 알 수 있음

  5. Learning rate 찾아가는 단계

     • 전체 training set을 활용하여 모델을 훈련시킴

       1. Learning rate를 매우 작은 숫자로 설정할 경우 (ex. lr = 1e-6 )

          👉 현상 : 보통 Loss값은 잘 변하지 않음, 그럼에도 불구하고 training set과 validation set에 대한 accuracy는 증가하는 모습을 보임

       2. Learning rate를 매우 큰 숫자로 설정할 경우 (ex. lr = 1e6 )

          👉 현상 : Loss값이 NaN을 가짐, 또는 마지막에 Inf를 가짐

     • cross validation을 통해서 정확한 Learning rate을 결정한다

Hyperparameter Optimization

• Cross-validation :

  • training set으로 학습시키고 validation set으로 평가하는 방법
  • 전략 – Coarse하게 시작하고 Fine하게 튜닝해 나가자
    • Coarse : Epoch 수를 작은 숫자를 줘서 대략적인 Hyperparameter 설정값에 대해 감을 잡음
    • Fine : Epoch 수를 좀 더 크게 줘서 세부적인 Hyperparameter seaching을 함

• Learning rate는 gradient와 곱해지기 때문에 선택범위를 log scale을 사용하는 편이 좋다.

• Random search Grid search

  • Grid search : Hyperparameter를 고정된 값과 간격으로 샘플링하는 것

  • Random search :

    • 처음에 대략적 범위를 설정 lr = 10**random.uniform(-3, 6) , reg = 10**random.uniform(-5, 5)

      ​ 👉 10** 을 해줌으로써 log space화를 해줌

    • 결과에 근거하여 범위를 줄여 나감

      

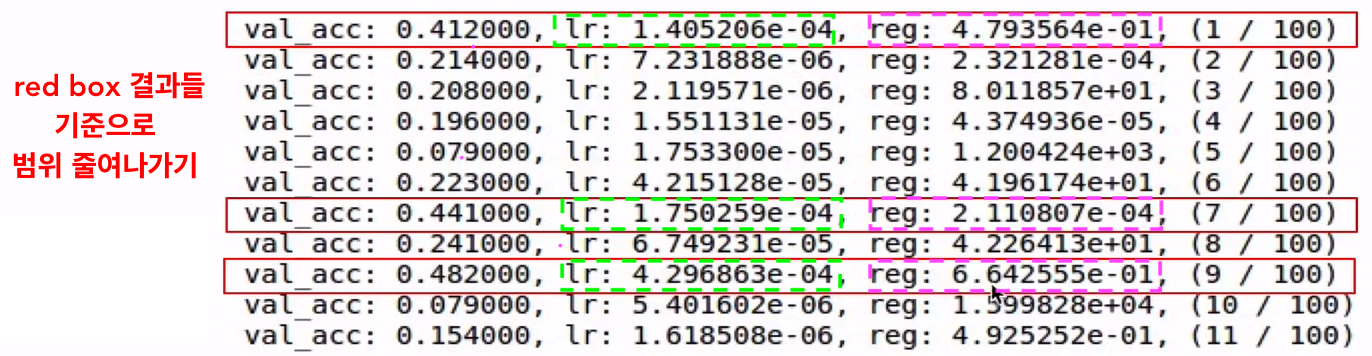
      ​ 👉 lr = 10**random.uniform(-3, -4) , reg = 10**random.uniform(-4, 0) 로 변경

  • Grid search 보다는 Random search를 하는 것이 더 Good

• Loss curve 모니터링

  

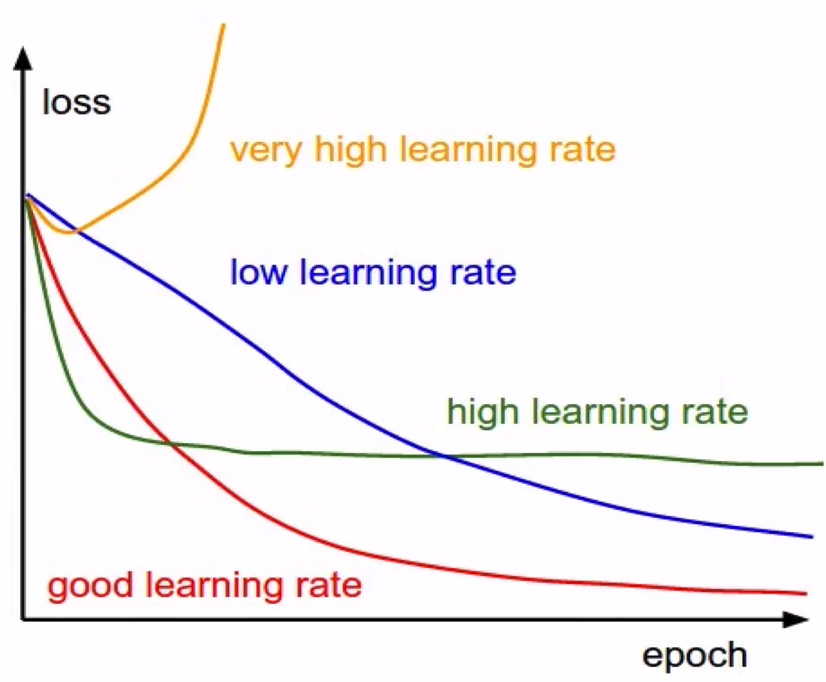
• Accuracy curve 모니터링

  

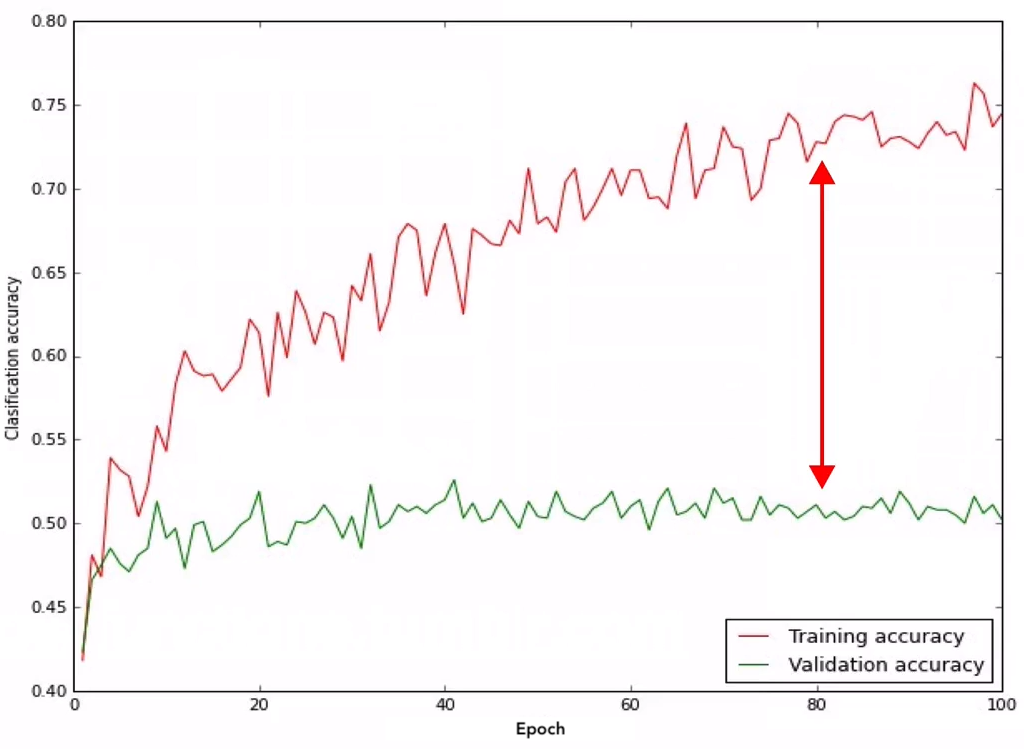
  • 수치의 해석이 가능해서 선호함
  • Traning accuracy와 Validation accuracy에는 Gap이 생김
    • 만약 Gap이 너무 크다면 Overfitting 의심해봐야됨 👉 regularization를 강화하기
    • 만약 Gap이 너무 작다면 아직 Overfit하지 않은 것이고 capacity을 높힐 수 있는 충분한 여유가 있다는 것을 의미함

Parameter update

• Stochastic Gradient Descent(SGD)는 weight를 찾아가는 과정 매우 느림

  """
  lr : Learning rate
  dx : Gradient
  """
  while True:
   dataBatch = dataset.sample_dataBatch()
   loss = network.forward(dataBatch)
   dx = network.backward()
   x = x + (-lr*dx) # Gradient descent update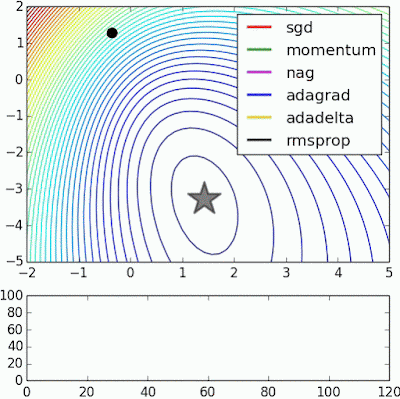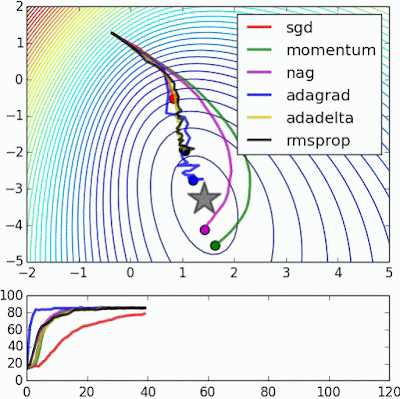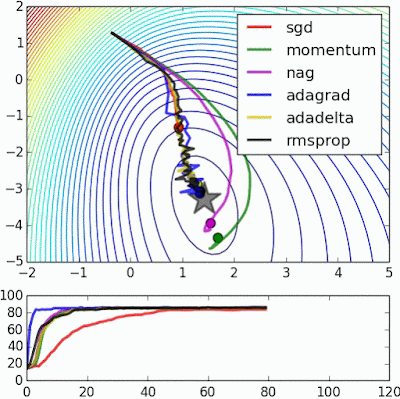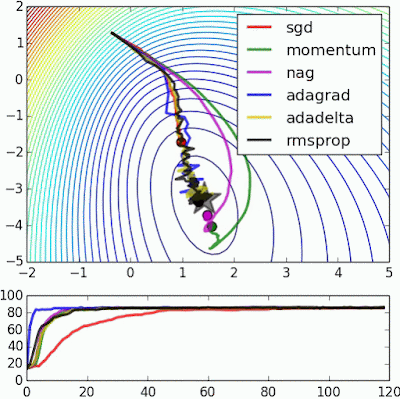
  

  

• 1st Order Optimization Method : Loss Function를 구하는데 있어서 gradient 정보만 사용

  1. Momentum

     # Momentum update
     velocity = mu*velocity - lr*dx
     x = x + velocity
     

     • mu : 마찰 계수(점차 속도가 느려지게 진행되도록 해줌) 보통 0.5, 0.6, 또는 0.99로 설정
     • 속도velocity를 일단 업데이트 해주고, x의 위치를 속도를 통해서 업데이트 해줌
       • 언덕에서 공을 굴리는 상황을 연상하면됨
       • 경사가 낮은 지점에서는 속도가 천천히 build up 됨
     • SGD보다 빠르게 찾아감

  2. Nesterov Accelerated Gradient (NAG)

     • Momentum보다 항상 convergence rate가 더 좋다

     • Momentum step : mu*velocity

     • Gradient step : lr*dx

     • Gradient step을 계산하기 전에 Momentum step을 미리 고려를 해서 시작점을 Momentum step의 종료점으로 변경한 다음 gradient step을 평가하는 방식

       

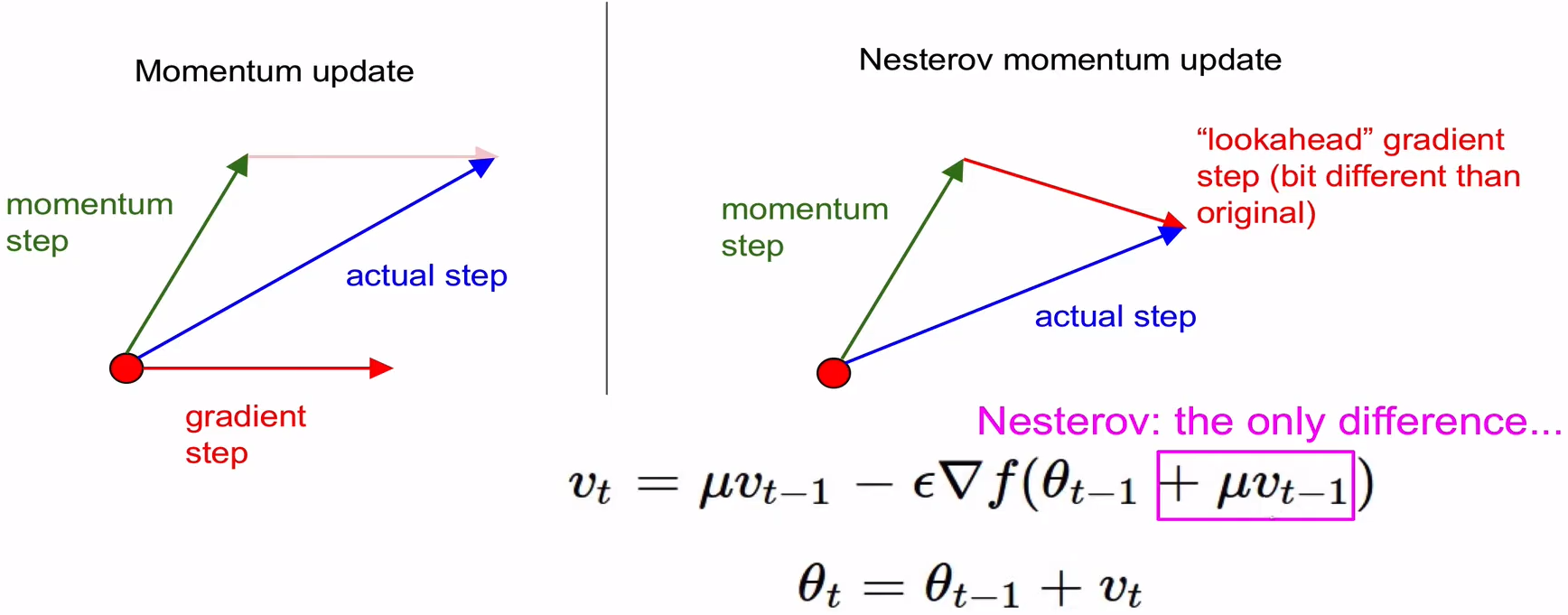
     • forward/backward 과정에서 불편한 점 :

       Momentum : parameter vector θ 와 그 위치에서의 gradient를 구하게됨

       NAG : parameter vector θ 와 parameter vector와 다른 위치에서의 gradient를 요구함

       💁🏻 해결방안 :

       

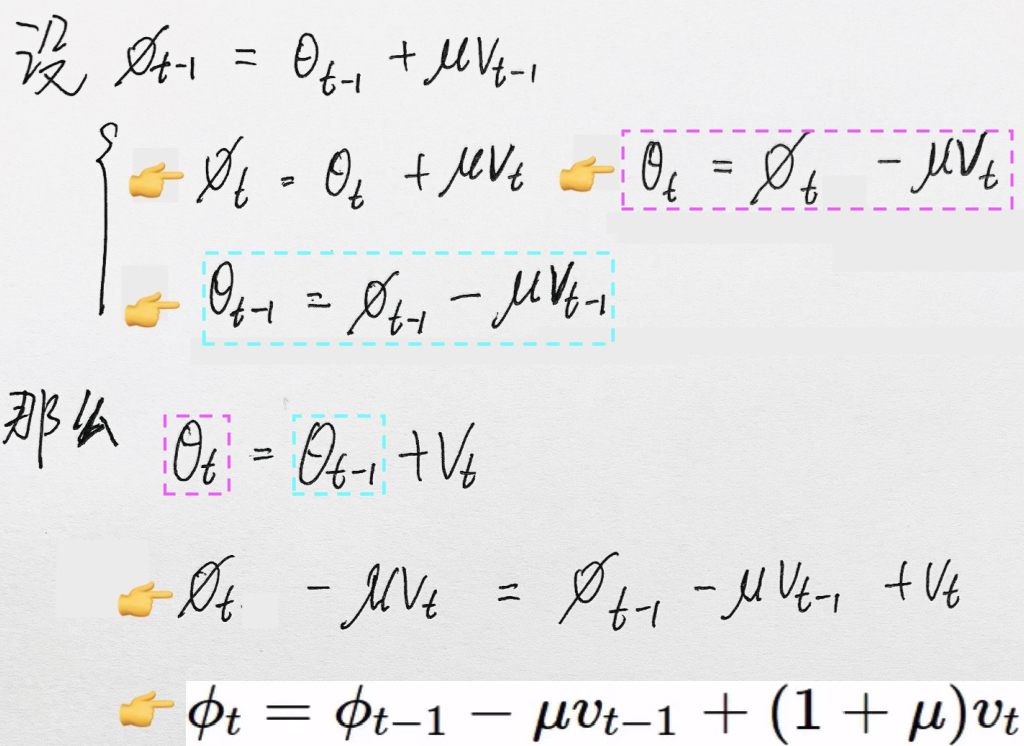
       # Nestrov Momentum update
       velocity_prev = velocity
       velocity = mu*velocity - lr*dx
       x = x + -mu*velocity_prev + (1+mu)*velocity
       

  3. AdaGrad

     # AdaGrad update
     cache = cache + dx**2
     x = x + (-lr*dx / (np.sqrt(cache)+1e-7))
     

     • cache : 계속 증가하게되는 양수, parameter vector와 동일한 size의 거대한 vector
     • Per-parameter adaptive learning rate method : 모든 parameter들이 동일한 learning rate를 적용받는게 아니라, cache가 계속 building up 되면서 하나 하나의 parameter들이 다 다른 값의 learning rate와 같은 영향을 받게됨
     • 1e-7 : 0으로 나누는 일을 방지하기 위한 역할
     • 문제점 : cache가 계속 building up 되면서 결국 step size가 0에 가까워져서 조기에 학습이 종료되는 상황이 발생하게 됨

  4. RMSProp

     • AdaGrad 업데이트 중 학습이 종료되지 않게 하기 위해 어떤 “에너지”를 제공

     # RMSProp
     cache = decay_rate*cache + (1-decay_rate)*dx**2
     x = x + (-lr*dx / (np.sqrt(cache)+1e-7))
     

     • decay_rate : step의 속도를 가속/감속 시킬 수 있다

  5. Adam – Good default choice 👍

     # Adam
     m,v = #... initialize caches to zeros
     for t in xrange(1, big_number):
       m = beta1*m + (1-beta1)*dx            # Momentum-like
       v = beta2*v + (1-beta2)*(dx**2)       # RMSProp-like
       mb = m/(1-beta1**t)	# bias correction
       vb = v/(1-beta2**t) # bias correction
       x = x + (-lr*mb / (np.sqrt(vb)+1e-7)) # RMSProp-like
     

     • Momentum + RMSProp 결합한 형태

     • beta1, beta2 : hyperparameter로써 보통 0.9, 0.99 으로 설정

     • bias correction : 초기 iteration 단계에서 m, v를 scaling up 해주는 역할

• 위의 방안들이 모두 learing rate lr 를 hyperparameter로 가지는데 어떠한 learing rate를 가지는게 최선일까?

  • 초기에는 큰 learing rate를 적용하고 서서히 learing rate를 작게 만들어 적용할 수 있게하도록

    • 方法1 – Step Decay : 한 Epoch마다 learing rate를 일정한 간격으로 감소시켜주는 방법
    • 方法2 – Exponential Decay :
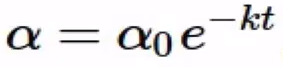
    • 方法3 – 1/t Decay :

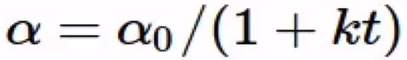
• 2nd Order Optimization Method : Hessian을 통해서 경사뿐만 아니라 곡면이 어떻게 구성되었는지 알 수 있음

  • 곡면이 어떻게 구성되었는지 알면 학습 필요없이 바로 최저점으로 갈 수 있음

  

  • 장점 :

    • learing rate가 필요 없게됨
    • 수렴이 빨라진다

  • Deep 한 Neural Network에서는 연산량이 너무 많아 현실적으로 사용불가 :

    • 만약에 parameter를 1억개를 가지는 Neural Network일 경우, Hessian는 1억×1억의 matrix를 가지게 됨
    • 게다가 이 matrix를 inverse 해야됨

  • 2nd Order Optimization Method를 사용하기 위한 접근법들

    • BGFS

      장점 : Hessian matrix를 inverse하는 대신에 rank 1의 Hessian을 inverse함으로써 연산을 줄임

      단점 : 여전히 메모리에 저장, 큰 Network에선 아직 동작하기 어려움

    • Limited memory BGFS

      장점 : 메모리에 저장하지

      단점 : 일반적으로 full-batch일 땐 잘 동작, Mini-batch 환경에선 잘 동작

  Regularization

  • Dropout

    

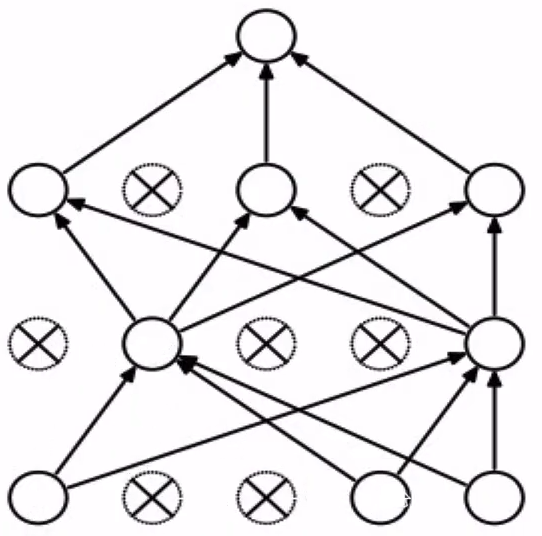
    probability = 0.5  # dropout확률 설정
    def train_step(X): # X는 data
      Hidden1 = np.maximum(0, np.dot(Weight1, X)+bias1)       # Activation Func : ReLU
      Mask1 = np.random.rand(*Hidden1.shape) < probability 
      Hidden1 = Hidden1 * Mask1 # 0으로 설정된 node는 drop됨!
      Hidden2 = np.maximum(0, np.dot(Weight2, Hidden1)+bias2) # Activation Func : ReLU
      Mask2 = np.random.rand(*Hidden2.shape) < probability 
      Hidden2 = Hidden2 * Mask2 # 0으로 설정된 node는 drop됨!
      out = np.dot(Weight3, Hidden2)+bias3
          
      # backward pass : compute gradient...
      # perform parameter update...
    

    • Forward pass 과정에서 일부 뉴런을 0으로 만드는 것 (Forward pass iteration 마다 모양은 계속 바뀜)

    • Mask : 각 node가 0 아니면 1이 되도록 설정해주는 역할 (probability보다 작으면 0 아님 1이 됨)

      • numpy.random.rand() 메소드를 사용하여(x1, ... ,xn)모양의 n차원 랜덤 배열을 생성
      • *Hidden.shape : tuple unpacking Code Example

    • 랜덤하게 일부 node들을 0으로 설정 = 연결이 끊킨거나 다름없음

    • 근데 Drop을 하는게 왜 좋음?

      👉 Network 내의 각 node가 한 부분만 집중적으로 관찰하는게 아니라 약간씩 중복을 가지면서 모든 것을 같이 관찰하는 모습을 보이면서 성능이 좋아짐

      

      👉 Overfitting을 어느정도 막아준다.

      👉 단일 모델로 앙상블(여러 개의 모델 에서 나온 값을 평균하는거) 효과를 가질 수 있다

      ​ 여러 개의 모델 = Forward pass iteration 마다 모양이 계속 바뀜

    • Testing stage :

      💁🏻 Monte Carlo approximation 방법 : Testing stage에도 Dropout를 그대로 활용, 그래서 각각의 Dropout에 대해서 평균을 낸 예측방법 , 비효율적인 방법

      💁🏻 Dropout을 사용하지 않는 방법 :

      ​ Testing stage 때는 모든 neuron들은 turn on!

      ​ 대신 activation 값들을 training stage 때의 probability 만큼 scaling을 해줘야됨

      def predict(X):
        Hidden1 = np.maximum(0, np.dot(Weight1, X)+bias1) * probability
        Hidden2 = np.maximum(0, np.dot(Weight2, Hidden1)+bias2) * probability
        out = np.dot(Weight3, Hidden2)+bias3
      

      이유 : Training stage / Testing stage 때 의 예측값이 서로 상이하다.

      ​ Example. probability 가 0.5 (== 1/2)일 경우

      ​

      ​ 💁🏻 Inverted Dropout 방법 :

      • Scaling을 Testing stage 에 안하고 Training stage 에 처리해줌

      probability = 0.5  
      def train_step(X): 
        Hidden1 = np.maximum(0, np.dot(Weight1, X)+bias1) / probability       # Scaling      
        Mask1 = np.random.rand(*Hidden1.shape) < probability 
        Hidden1 = Hidden1 * Mask1 
        Hidden2 = np.maximum(0, np.dot(Weight2, Hidden1)+bias2) / probability # Scaling 
        Mask2 = np.random.rand(*Hidden2.shape) < probability 
        Hidden2 = Hidden2 * Mask2 
        out = np.dot(Weight3, Hidden2)+bias3
              
        # backward pass : compute gradient...
        # perform parameter update...
              
       def predict(X):
        Hidden1 = np.maximum(0, np.dot(Weight1, X)+bias1)       # No Scaling 
        Hidden2 = np.maximum(0, np.dot(Weight2, Hidden1)+bias2) # No Scaling 
        out = np.dot(Weight3, Hidden2)+bias3
      

    • 참고 : 최근에 Batch Normalization쓰는 경우 Dropout를 잘 사용하지

《Reference》

1. Youtube
2. Blog
3. Course Site