Collaborative Filtering

Basic Idea

• 사용자 x한테 추천을 해주고 싶으면 사용자 x랑 비슷하게 rating을 한 이웃들 N을 먼저 찾는다

• 그리고 사용자 x의 rating을 이웃들 N을 근거해서 예측하는 것 이다

  

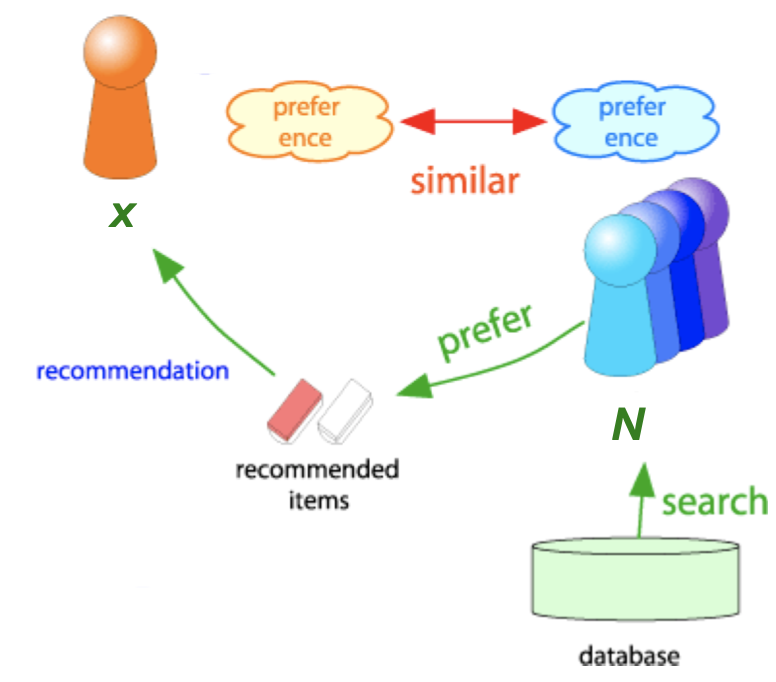
Q1 : 사용자 x의 rating이랑 비슷한 이웃들 N을 어떻게 찾을까?

• 사용자 A,B,C,D 가 있고 각 사용자들이 영화 Harry Potter[1],[2],[3]; Twilight; Star Wars[1],[2],[3]를 rating한 데이터가 있다고 하자. (rating은 0~5까지만 있다, 빈칸은 not rated를 나타낸다)

  

• 앞으로 “r_x” 은 사용자 x의 rating의 벡터를 나타내는데 사용된다

• Similarity Function은 “이 빈칸을 어떻게 대할건지?”가 관점이 되겠다

• 사용자 A의 rating을 기준으로 사용자 B랑 공통적으로 rating한 영화는 “Harry Potter[1]” 1개 밖에 없다.”Harry Potter[1]” rating 점수를 보면 사용자 A,B 모두 “Harry Potter 1”에 대해 좋은 rating을 줬다

• 사용자 A의 rating을 기준으로 사용자 C랑 공통적으로 rating한 영화는 “Twilight, Star Wars[1]” 2개다. “Twilight” rating 점수를 보면 사용자 A는 좋은 rating을 주었지만 사용자 C는 좋지못한 rating을 주었다. 반면에 “Star Wars[1]” rating 점수를 보면 사용자 C는 좋은 rating을 주었지만 사용자 A는 좋지못한 rating을 주었다.

• 그래서 직관적으로 봤을 때, 사용자 A & 사용자 B의 Similarity는 사용자 A & 사용자 C의 Similarity보다 더 높다는 걸 알 수 있다

• 그럼 Similarity 값을 알아내기 위한 Similarity Function들을 살펴보자

  • 1) Jaccard Similarity :

    

    • 사용자 A & 사용자 B의 Similarity = 공통 1개 영화 / 총 5개 영화 = 1/5

    • 사용자 A & 사용자 C의 Similarity = 공통 2개 영화 / 총 4개 영화 = 2/4

    • 즉, 사용자 A & 사용자 B의 Similarity < 사용자 A & 사용자 C의 Similarity

      ➡️ (처음에 우리가 생각한거랑 다른 결과)

    • ⚠️ Jaccard Similarity는 각 rating 값을 신경쓰지 않는다는 문제가 있다

  • 2) Cosine Similarity :

    

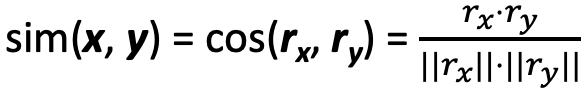
    • 이때 “빈칸 rating은 0점” 으로 생각하고 계산한다

      Vector	Value
      r_A	{4, 0, 0, 5, 1, 0, 0}
      r_B	{5, 5, 4, 0, 0, 0, 0}
      r_C	{0, 0, 0, 2, 4, 5, 0}

    • 사용자 A & 사용자 B의 Similarity : 0.38 = \({(4 \times 5)} + {(0 \times 5)} + {(0 \times 4)} + {(5 \times 0)} + {(1 \times 0)} + {(0 \times 0)} + {(0 \times 0)} \over {\sqrt{4^2 + 5^2 + 1^2}} . {\sqrt{5^2 + 5^2 + 4^2}}\)

    • 사용자 A & 사용자 C의 Similarity : 0.32 = \({(4 \times 0)} + {(0 \times 0)} + {(0 \times 0)} + {(5 \times 2)} + {(1 \times 4)} + {(0 \times 5)} + {(0 \times 0)} \over {\sqrt{4^2 + 5^2 + 1^2}} . {\sqrt{2^2 + 4^2 + 5^2}}\)

    • 즉, 사용자 A & 사용자 B의 Similarity > 사용자 A & 사용자 C의 Similarity

      ➡️ (처음에 우리가 생각한거랑 같은 결과)

    • ⚠️ Cosine Similarity에서 “빈칸 rating은 0점” 으로 생각하고 계산했다는 것 은 아직 평가하지 않은 영화 인데도 불구하고 모두 최하점수 0으로 부여했다는 사실이 문제점이 된다

  • 3) Centered Cosine Similarity (Pearson correlation coefficient) :

    

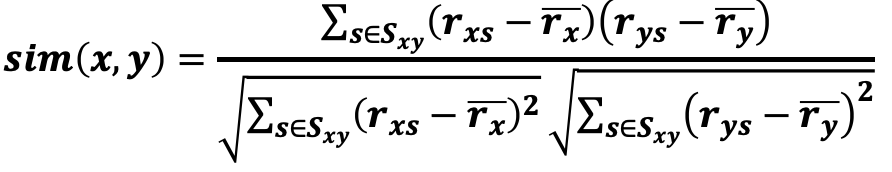
  • 먼저 각 사용자의 rating 평균을 구한다

    평균	Value
    S_A	(4+5+1) / 3 = 10/3
    S_B	(5+5+4) / 3 = 14/3
    S_C	(2+4+5) / 3 = 11/3

  • Normalize해주기 위해 각 Rating 값에서 대응하는 사용자의 rating 평균을 빼준다

    

    

    ➡️ 여기서 각 Row의 rating값을 더하면 모두 0이 나온다

    ➡️ 즉, 우리가 한 것은 모든 사용자의 rating 중간을 0이 되도록 만들었다

    ➡️ 그래서 양수일 경우 rating 이 좋다는 의미고 음수일 경우 rating이 안좋다는 의미다

  • 그 다음, Normalize된 rating값들을 Cosine Similarity로 구해 주면 된다

    • 사용자 A & 사용자 B의 Similarity : 0.09

    • 사용자 A & 사용자 C의 Similarity : - 0.56

    • 즉, 사용자 A & 사용자 B의 Similarity > 사용자 A & 사용자 C의 Similarity

      ➡️ (처음에 우리가 생각한거랑 같은 결과)

Q2 : 사용자 x와 비슷한 이웃들 N을 찾았으면 사용자 x의 영화 i 에 대한 rating 값을 어떻게 예측할까?

• 이웃들 N를 k명 찾았다고 하자

  • 1) Average :

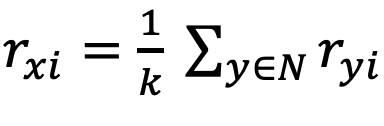
    • “이웃y가 영화 i 한테 부여한 rating값” 들 의 합 / 총 이웃 k명

    • ⚠️ 이렇게 계산할 경우 사용자와 이웃 간의 Similarity value를 무시하게 된다

  • 2) Weighted Average :

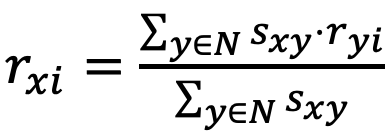
    • “이웃y랑 사용자x 간의 Similarity value * 이웃y가 영화i 한테 부여한 rating값” 들 의 합 / “이웃y랑 사용자x 간의 Similarity value” 들 의 합
    • ⚠️ 이웃y가 영화i 한테 부여한 rating값에다 Similarity value로 가중치를 부여하여서 관련있는 rating값은 크게 적용되고 관련없는 rating값은 적게 적용될 수 있도록 하였다

Q3 : User-user Collaborative filtering 외에 다른 관점에서의 Collaborative filtering은 어떻게 하나?

• User-user : Similarity value를 구할 때 사용자와 사용자 간의 유사도를 구했다

• Item-item : 이번에 아이템과 아이템 간의 유사도를 구해보자

  

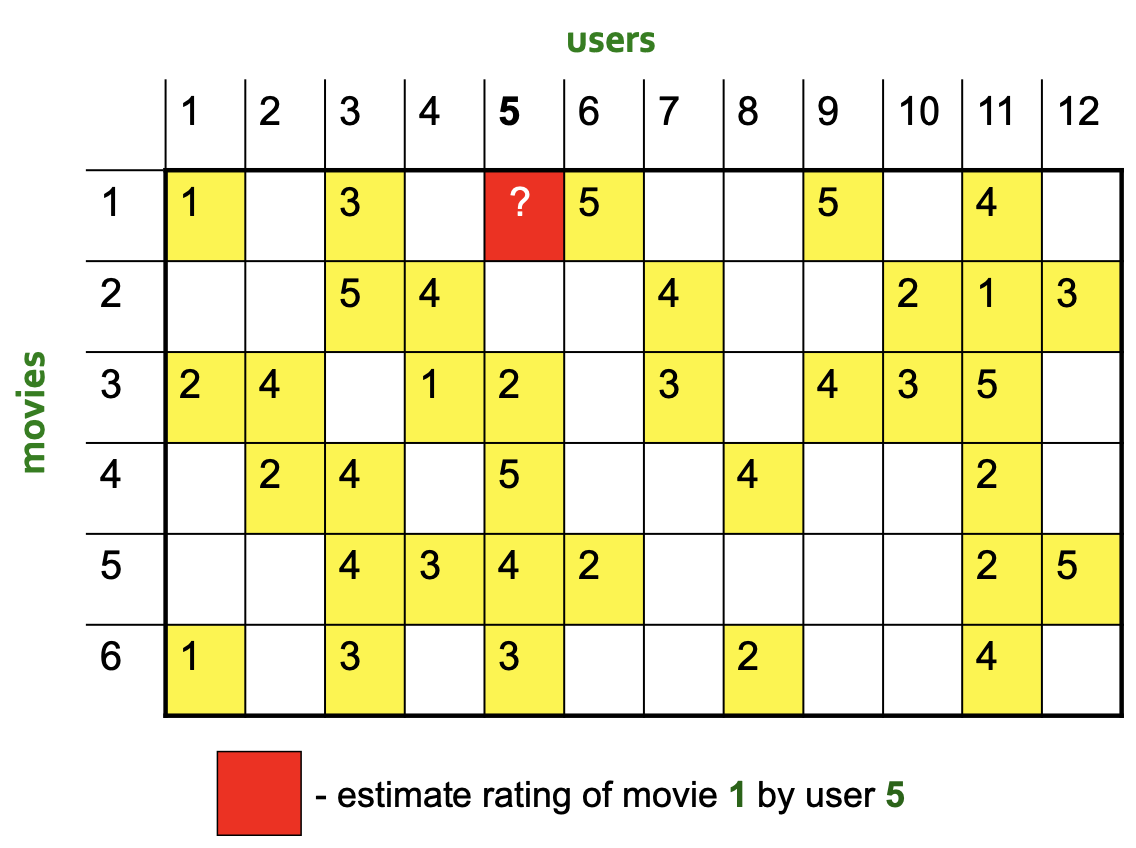
  • 먼저 유사한 item을 2개만 고른다고 하자. Centered Cosine Similarity를 가지고 item 1과 나머지 item들 간의 Similarity를 각각 구한 다음 Similarity value가 높은 2개 item을 선택하면 된다

    

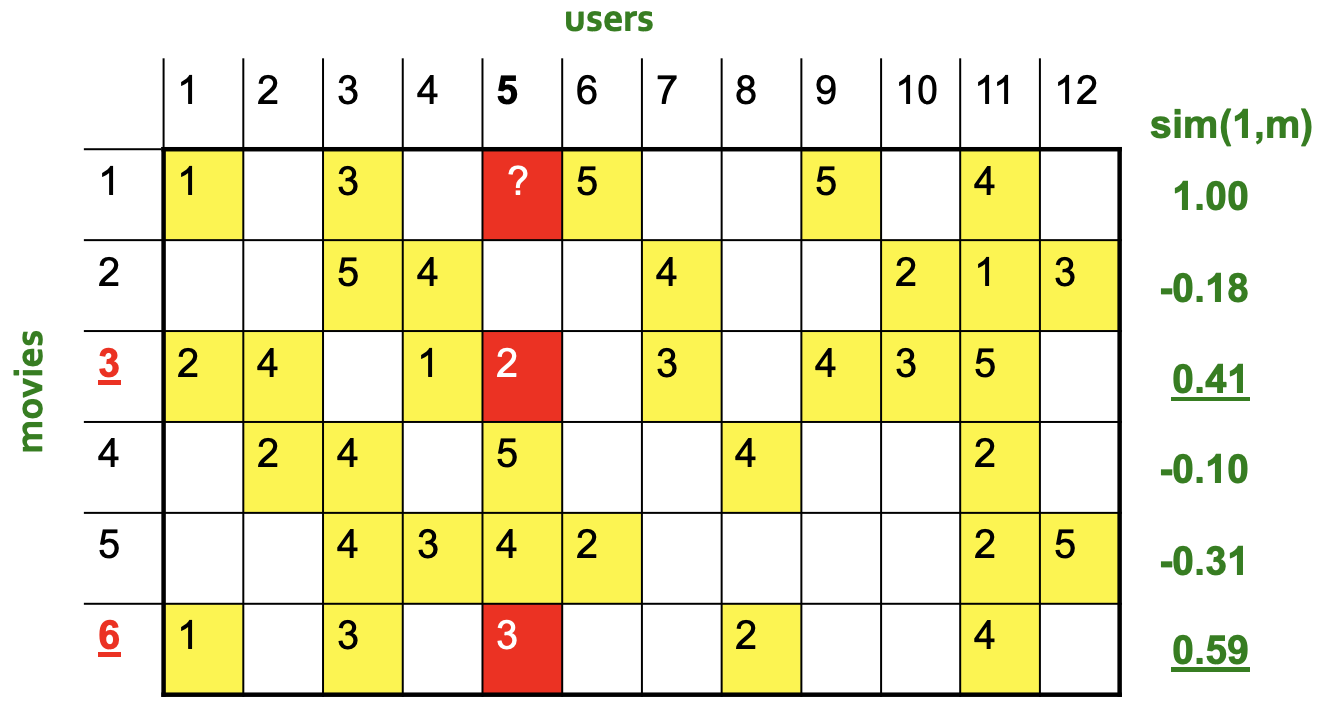
  • 그 다음 Weighted Average를 통해 user 5가 매긴 movie 1의 rating 값을 알아낼 수 있다

    

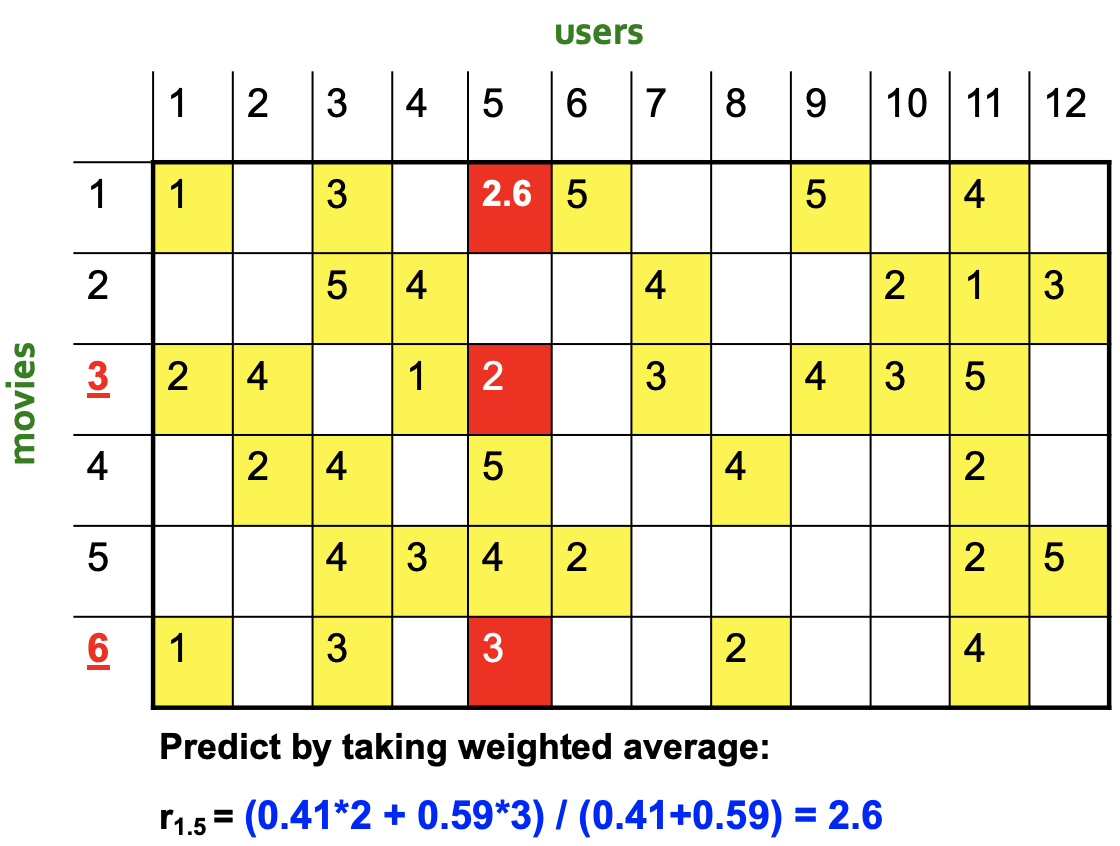
• Collaborative filtering 같은 경우,보통 Item-item이 User-user 보다 더 잘 예측할 수 있다

  ➡️ Why? Items are simpler, users have multiple tastes

CF의 장단점

장점	단점
책, 음악, 동영상 등등 어떠한 아이템에도 적용할 수 있다	Cold Start : 처음 시작할 때 데이터가 부족하기 때문에 올바를 추천을 할 수 없다
	Sparsity : 만약에 사용자x가 아이템i에 대한 rating 점수를 예측하고자 할 때, 다른 사용자들이 아이템i에 대한 rating 점수를 알아야되는데, 점수들이 잘 없을 경우 예측이 힘듬
	First data problem : 새로운 아이템이 추가되었으면 이 아이템은 어느 사용자한테도 추천해 줄 수가 없다 (왜냐면 새로운 아이템은 아무런 rating이 없으니깐). 인기가 없는 제품도 포함된다.
	Poplularity bias : Harry Potter 같은 명작은 많은 사람들이 좋은 점수를 줄 것 이다. 그래서 Collaborative filtering는 사용자가 좋아하든 싫어하든 대부분한테 Harry Potter를 추천해줄 수 밖에 없다 (Harry Potter가 많은 량의 좋은 평가가 있으니 어느 영화랑 엮일 수 있으니깐)

Hybrid Methods :

• Collaborative filtering의 단점을 좀 극복해 줄 수 있는 방법

• 方法1 ： Collaborative filtering 에다 Content-based methods를 추가한다

• 方法2 ：2개 이상의 다른 Recommender들을 구현한 다음 예측을 합친다

  Ex) Global Baseline + Collaborative Filtering :

  [Problem] Joe가 The Six Sense라는 영화를 몇 점에 평가할 지 예측 해볼려고 하는데 The Six Sense라는 영화하고 비슷한 영화들에 대해서도 아무런 평가를 하지 않았다. (즉 Collaborative filtering의 Sparsity Problem)

  • Global Baseline :
    • 예를 들어 모든 사용자가 모든 영화에 대해 rating한 값의 평균이 3.7점이라 하자
    • The Six Sense의 평균 rating은 4.2점이라 하자 (전체 영화 평균보다 0.5점이 높음)
    • Joe가 좀 터프한 평가자이라서 그런지 여태 rating했던 점수들의 평균이 3.5점이라 하자 (전체 영화 평균보다 0.2점이 낮음)
    • 위에 정보를 모두 합쳐보면 Baseline Estimate를 구할 수 있다 : 3.7 + 0.5 - 0.2 = 4점
  • Collaborative Filtering :
    • The Six Sense와 가장 유사한 영화를 찾았더니 Signs가 있었고
    • Joe는 Signs라는 영화에게 2.5점을 주었다 (Joe의 평균 rating보다 1점이 낮음)
  • Global Baseline + Collaborative Filtering :
    • Baseline Estimate과 Collaborative Filtering의 정보를 합쳐서 최종 예측을 얻을 수 있다 :
      • Joe는 The Six Sense 영화에 4 - 1 = 3점을 부여할 것이다.

  • 공식화할 경우